Hadamard-Transformation

Die Hadamard-Transformation, auch bezeichnet als Walsh-Hadamard-Transformation, Hadamard-Rademacher-Walsh-Transformation, Walsh-Transformation und als Walsh-Fourier-Transformation, ist eine diskrete Transformation aus dem Bereich der Fourier-Analysis. Sie ist eine orthogonal-symmetrische, selbstinverse und lineare Transformation und von der Struktur her verwandt mit der diskreten Fourier-Transformation (DFT). Die Hadamard-Transformation bildet einen Satz von 2 m {\displaystyle 2^{m}} reellen oder komplexen Eingangswerten in einen Bildbereich aus überlagerten Walsh-Funktionen, dem Walsh-Spektrum, ab.[1] Die Transformation ist benannt nach den Mathematikern Jacques Hadamard, Joseph L. Walsh und Hans Rademacher.

Die Anwendungen der Hadamard-Transformation liegen im Bereich der digitalen Signalverarbeitung und Datenkompression wie beispielsweise bei JPEG XR und H.264/MPEG-4 AVC.

Definition

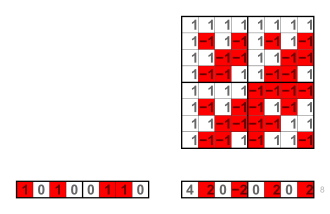
Das Produkt einer binären Eingangsfolge und einer 2 m × 2 m {\displaystyle 2^{m}\times 2^{m}} -Hadamard-Matrix ergibt das Walsh-Spektrum:
(1,0,1,0,0,1,1,0) * H(8) = (4,2,0,−2,0,2,0,2)

Die Hadamard-Transformation H m {\displaystyle \operatorname {H} _{m}} wird aus einer 2 m × 2 m {\displaystyle 2^{m}\times 2^{m}} -Hadamard-Matrix, skaliert mit einem Normalisierungsfaktor, gebildet, welche eine Eingangsfolge ( x n ) {\displaystyle (x_{n})} der Länge 2 m {\displaystyle 2^{m}} mittels einer Matrix-Vektor-Multiplikation in eine Ausgangsfolge ( X k ) {\displaystyle (X_{k})} transformiert.

Die Hadamard-Transformation kann verschiedenartig definiert werden, unter anderem rekursiv, wobei von einer 1 × 1 {\displaystyle 1\times 1} -Hadamard-Transformation H 0 {\displaystyle \operatorname {H} _{0}} mit der Identität H 0 = 1 {\displaystyle \operatorname {H} _{0}=1} ausgegangen wird und H m {\displaystyle \operatorname {H} _{m}} für m > 0 {\displaystyle m>0} festgelegt wird zu:

H m = 1 2 ( H m − 1 H m − 1 H m − 1 − H m − 1 ) {\displaystyle \operatorname {H} _{m}={\frac {1}{\sqrt {2}}}{\begin{pmatrix}\operatorname {H} _{m-1}&\operatorname {H} _{m-1}\\\operatorname {H} _{m-1}&-\operatorname {H} _{m-1}\end{pmatrix}}}

mit dem Normalisierungsfaktor 1 2 {\displaystyle {\tfrac {1}{\sqrt {2}}}} , der mitunter auch weggelassen wird.

Analog wie bei der diskreten Fourier-Transformation (DFT) und der optimierten schnellen Fourier-Transformation (FFT) existiert auch eine schnelle Hadamard-Transformation, welche die Anzahl n {\displaystyle n} der Operationen auf n ⋅ log ⁡ ( n ) {\displaystyle n\cdot \operatorname {log} (n)} mit n = 2 m {\displaystyle n=2^{m}} reduziert.

Zusammenhang zur diskreten Fouriertransformation

Wie auch die Hadamard-Transformation lässt sich die diskrete Fourier-Transformation als Produkt einer Transformationsmatrix und eines Eingangsvektors formulieren. Sollen per DFT N = 2 {\displaystyle N=2} Elemente im Zeitbereich in den Spektralbereich transformiert werden, so lautet die DFT-Matrix

F 2 = [ 1 1 1 − 1 ] {\displaystyle F_{2}={\begin{bmatrix}1&1\\1&-1\end{bmatrix}}} .

Die Hadamard-Matrix ohne Skalierungsfaktor ist dann als Kronecker-Produkt aus einzelnen 2 × 2 {\displaystyle 2\times 2} DFT-Matrizen konstruierbar:

H 2 k = [ 1 1 1 − 1 ] ⊗ [ 1 1 1 − 1 ] ⊗ [ 1 1 1 − 1 ] ⊗ … ⊗ [ 1 1 1 − 1 ] ⏟ k  mal {\displaystyle H_{2^{k}}={\underset {k{\text{ mal}}}{\underbrace {{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}\otimes {\begin{bmatrix}1&1\\1&-1\end{bmatrix}}\otimes {\begin{bmatrix}1&1\\1&-1\end{bmatrix}}\otimes \ldots \otimes {\begin{bmatrix}1&1\\1&-1\end{bmatrix}}} }}} .

Literatur

  • Kathy J. Horadam: Hadamard Matrices and their Applications. Princeton University Press, Princeton NJ u. a. 2007, ISBN 978-0-691-11921-2. 

Einzelnachweise

  1. ↑ Henry O. Kunz: On the Equivalence Between One-Dimensional Discrete Walsh-Hadamard and Multidimensional Discrete Fourier Transforms. In: IEEE Transactions on Computers. Bd. 28, Nr. 3, 1979, ISSN 0018-9340, S. 267–268, doi:10.1109/TC.1979.1675334.