Circuito RLC

En electrodinámica, un circuito RLC es un circuito lineal que contiene una resistencia eléctrica, una bobina y un capacitor.

Existen dos tipos de circuitos RLC, en serie o en paralelo, según la interconexión de los tres tipos de componentes. El comportamiento de un circuito RLC se describe generalmente por una ecuación diferencial de segundo orden (en donde los circuitos RC o RL se comportan como circuitos de primer orden).

Con ayuda de un generador de señales, es posible inyectar en el circuito oscilaciones y observar en algunos casos el fenómeno de resonancia, caracterizado por un aumento de la corriente (ya que la señal de entrada elegida corresponde a la pulsación propia del circuito, calculable a partir de la ecuación diferencial que lo rige).

Circuito RLC en serie

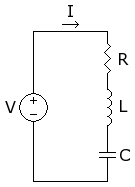
Circuito sometido a un escalón de tensión

Si un circuito RLC en serie es sometido a un escalón de tensión ${\displaystyle E\,}$, la ley de las mallas impone la relación:

${\displaystyle E=u_{C}+u_{L}+u_{R}=u_{C}+L{\frac {di}{dt}}+R_{t}i}$

Introduciendo la relación característica de un condensador:

${\displaystyle i_{C}=i=C{\frac {du_{C}}{dt}}}$

Se obtiene la ecuación diferencial de segundo orden:

${\displaystyle E=u_{C}+LC{\frac {d^{2}u_{C}}{dt^{2}}}+R_{t}C{\frac {du_{C}}{dt}}}$

donde:

• E es la fuerza electromotriz de un generador, en Voltios (V);
• u_C es la tensión en los bornes de un condensador, en Voltios (V);
• L es la inductancia de la bobina, en Henrios (H);
• i es la intensidad de corriente eléctrica en el circuito, en Amperios (A);
• q es la carga eléctrica del condensador, en Coulombs (C);
• C es la capacidad eléctrica del condensador, en Faradios (F);
• R_t es la resistencia total del circuito, en Ohmios (Ω); y
• t es el tiempo en segundos (s)

En el caso de un régimen sin pérdidas, esto es para ${\displaystyle R_{t}=0\,}$, se obtiene una solución de la forma:

${\displaystyle u_{c}=E\cos \left({\frac {2\pi t}{T_{0}}}+\varphi \right)}$

${\displaystyle T_{0}=2\pi {\sqrt {LC}}}$

donde:

• T₀ el periodo en segundos;
• φ la fase en el origen (lo más habitual es elegirla para que φ = 0).

Lo que resulta:

${\displaystyle f_{0}={\frac {1}{2\pi {\sqrt {LC}}}}}$

donde ${\displaystyle f_{0}}$ es la frecuencia de resonancia, en hercios (Hz).

Circuitos sometidos a una tensión sinusoidal

La transformación compleja aplicada a las diferentes tensiones permite escribir la ley de las mallas bajo la forma siguiente:

${\displaystyle {\underline {U_{G}}}={\underline {U_{R}}}+{\underline {U_{L}}}+{\underline {U_{C}}},}$

siendo ${\displaystyle {\underline {U_{G}}}}$ la tensión en el generador. Introduciendo las impedancias complejas:

${\displaystyle {\underline {U_{G}}}=R{\underline {I}}+j\omega L{\underline {I}}-{\frac {j}{\omega C}}{\underline {I}}={\bigg [}R+j\ {\frac {\omega ^{2}LC-1}{\omega C}}{\bigg ]}{\underline {I}}}$

La frecuencia angular (o pulsación) de resonancia de corriente de este circuito ω₀ es dada por:

${\displaystyle \omega _{0}={\frac {1}{\sqrt {LC}}}}$

Para esta frecuencia la relación de arriba se convierte en:

${\displaystyle {\underline {U_{G}}}={\underline {U_{R}}}=R{\underline {I}}}$

y se obtiene: ${\displaystyle {\underline {U_{L}}}=-{\underline {U_{C}}}={\frac {j}{R}}{\sqrt {\frac {L}{C}}}\ {\underline {U_{G}}}\,}$.

Circuito RLC en paralelo

${\displaystyle i_{r}={\frac {u}{R}}}$
${\displaystyle {\frac {di_{l}}{dt}}={\frac {u}{L}}}$
${\displaystyle i_{c}={\frac {dq}{dt}}=C{\frac {du}{dt}}}$

ya que ${\displaystyle q=Cu\,}$

${\displaystyle i=i_{r}+i_{l}+i_{c}\,}$

${\displaystyle {\frac {di}{dt}}=C{\frac {d^{2}u}{dt^{2}}}+{\frac {1}{R}}{\frac {du}{dt}}+{\frac {u}{L}}\,}$.

Atención: la rama C es un corto-circuito: de esta manera no se pueden unir las ramas A y B directamente a los bornes de un generador E, se les debe adjuntar una resistencia.

Las dos condiciones iniciales son:

• ${\displaystyle i_{l0}\,}$ conserva su valor antes de la puesta en tensión (porque la inductancia se opone a la variación de corriente).
• ${\displaystyle q_{0}\,}$ conserva su valor antes de la puesta en tensión ${\displaystyle u_{0}={\frac {q_{0}}{C}}}$.

Circuito sometido a una tensión sinusoidal

La transformación compleja aplicada a las diferentes intensidades proporciona:

${\displaystyle {\underline {I}}={\underline {I_{r}}}+{\underline {I_{l}}}+{\underline {I_{c}}}}$

Siendo, introduciendo las impedancias complejas:

${\displaystyle {\underline {I}}={\frac {1}{R}}{\underline {U}}+{\frac {1}{jL\omega }}{\underline {U}}+jC\omega {\underline {U}}}$

siendo : ${\displaystyle {\underline {I}}=\left[{\frac {1}{R}}+j(C\omega -{\frac {1}{L\omega }})\right]{\underline {U}}}$

La frecuencia angular de resonancia en intensidad de este circuito ω₀ es dada por:

${\displaystyle \omega _{0}={\frac {1}{\sqrt {LC}}}}$

Para esta frecuencia, la relación de arriba se convierte en:

${\displaystyle {\underline {I}}={\underline {I_{r}}}={\frac {1}{R}}{\underline {U}}}$

y se obtiene:

${\displaystyle {\underline {I_{c}}}=-{\underline {I_{l}}}=j{\sqrt {\frac {C}{L}}}{\underline {U}}\,}$.

Uso de los circuitos RLC

Los circuitos RLC son generalmente utilizados para realizar filtros de frecuencias, o de transformadores de impedancia. Estos circuitos pueden entonces comportar múltiples inductores y condensadores: se habla entonces de «red LC».

Un circuito LC simple es denominado de segundo orden porque su función de transferencia comporta un polinomio de segundo grado en el denominador.

Véase también

• Circuito RC
• Circuito RL
• Circuito LC

Enlaces externos

• Un vídeo explicativo sobre la resonancia de un circuito RLC
• Calculadora - Circuito RLC en régimen
• Animación (applet JAVA)
• Desarrollo matemático y oscilaciones amortiguadas en un circuito RLC serie Archivado el 22 de octubre de 2013 en Wayback Machine.