Beta Función de densidad de probabilidad Función de distribución de probabilidad Parámetros α > 0 {\displaystyle \alpha >0} real ) β > 0 {\displaystyle \beta >0} real ) Dominio x ∈ ( 0 , 1 ) {\displaystyle x\in (0,1)} Función de densidad (pdf) x α − 1 ( 1 − x ) β − 1 B ( α , β ) {\displaystyle {\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}\!} Función de distribución (cdf) I x ( α , β ) {\displaystyle I_{x}(\alpha ,\beta )\!} Media α α + β {\displaystyle {\frac {\alpha }{\alpha +\beta }}\!} Moda α − 1 α + β − 2 {\displaystyle {\frac {\alpha -1}{\alpha +\beta -2}}\!} α > 1 , β > 1 {\displaystyle \alpha >1,\beta >1} Varianza α β ( α + β ) 2 ( α + β + 1 ) {\displaystyle {\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}\!} Coeficiente de simetría 2 ( β − α ) α + β + 1 ( α + β + 2 ) α β {\displaystyle {\frac {2\,(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}} Función generadora de momentos (mgf) 1 + ∑ n = 1 ∞ ( ∏ r = 0 n − 1 α + r α + β + r ) t n n ! {\displaystyle 1+\sum _{n=1}^{\infty }\left(\prod _{r=0}^{n-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {t^{n}}{n!}}} Función característica 1 F 1 ( α ; α + β ; i t ) {\displaystyle {}_{1}F_{1}(\alpha ;\alpha +\beta ;i\,t)\!} [editar datos en Wikidata]
En teoría de la probabilidad y en estadística, la distribución beta es una familia de distribuciones continuas de probabilidad definidas en el intervalo ( 0 , 1 ) {\displaystyle (0,1)} α {\displaystyle \alpha } β {\displaystyle \beta }
La generalización de esta distribución a varias variables es conocida como la distribución de Dirichlet .
Definición Notación Si una variable aleatoria continua X {\displaystyle X} distribución beta con parámetros α , β > 0 {\displaystyle \alpha ,\beta >0} X ∼ B ( α , β ) {\displaystyle X\sim \mathrm {B} (\alpha ,\beta )}
Otras notaciones para la distribución beta usadas son X ∼ Beta ( α , β ) {\displaystyle X\sim \operatorname {Beta} (\alpha ,\beta )} X ∼ B e ( α , β ) {\displaystyle X\sim {\mathcal {Be}}(\alpha ,\beta )} X ∼ β α , β {\displaystyle X\sim \beta _{\alpha ,\beta }}
Función de densidad La función de densidad de X {\displaystyle X}
f X ( x ) = x α − 1 ( 1 − x ) β − 1 B ( α , β ) {\displaystyle f_{X}(x)={\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}} para valores 0 < x < 1 {\displaystyle 0<x<1} B ( α , β ) {\displaystyle \mathrm {B} (\alpha ,\beta )} función beta y se define para α , β > 0 {\displaystyle \alpha ,\beta >0}
B ( α , β ) = ∫ 0 1 x α − 1 ( 1 − x ) β − 1 d x {\displaystyle \mathrm {B} (\alpha ,\beta )=\int _{0}^{1}x^{\alpha -1}(1-x)^{\beta -1}dx} y algunas de las propiedades que satisface son:
B ( α , β ) = B ( β , α ) {\displaystyle \mathrm {B} (\alpha ,\beta )=\mathrm {B} (\beta ,\alpha )} B ( α , β ) = Γ ( α ) Γ ( β ) Γ ( α + β ) {\displaystyle \mathrm {B} (\alpha ,\beta )={\frac {\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}}} Función de distribución La función de distribución de X {\displaystyle X}
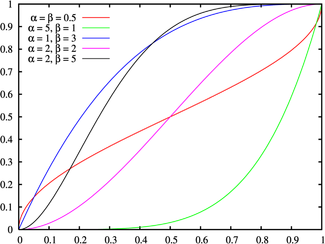
F X ( x ) = B ( x ; α , β ) B ( α , β ) = I x ( α , β ) {\displaystyle F_{X}(x)={\frac {\mathrm {B} (x;\alpha ,\beta )}{\mathrm {B} (\alpha ,\beta )}}=I_{x}(\alpha ,\beta )} donde B ( x ; α , β ) {\displaystyle \mathrm {B} (x;\alpha ,\beta )} función beta incompleta y I x ( α , β ) {\displaystyle I_{x}(\alpha ,\beta )} función beta incompleta regularizada .
Propiedades Si X ∼ B ( α , β ) {\displaystyle X\sim \mathrm {B} (\alpha ,\beta )} X {\displaystyle X}
Media La media de la variable aleatoria X {\displaystyle X}
E [ X ] = α α + β {\displaystyle {\text{E}}[X]={\frac {\alpha }{\alpha +\beta }}} Varianza La varianza de la variable aleatoria X {\displaystyle X}
Var ( X ) = α β ( α + β + 1 ) ( α + β ) 2 {\displaystyle {\text{Var}}(X)={\frac {\alpha \beta }{(\alpha +\beta +1)(\alpha +\beta )^{2}}}} Moda La moda de la variable aleatoria X {\displaystyle X}
α − 1 α + β − 2 {\displaystyle {\frac {\alpha -1}{\alpha +\beta -2}}} para valores de α , β > 1 {\displaystyle \alpha ,\beta >1}
Momentos El n {\displaystyle n} X {\displaystyle X}
E [ X n ] = B ( α + n , β ) B ( α + β ) = ∏ r = 0 n − 1 α + r α + β + r = α ( α + 1 ) ⋯ ( α + n − 1 ) ( α + β ) ( α + β + 1 ) ⋯ ( α + β + n − 1 ) {\displaystyle {\begin{aligned}{\text{E}}[X^{n}]&={\frac {\mathrm {B} (\alpha +n,\beta )}{\mathrm {B} (\alpha +\beta )}}\\&=\prod _{r=0}^{n-1}{\frac {\alpha +r}{\alpha +\beta +r}}\\&={\frac {\alpha (\alpha +1)\cdots (\alpha +n-1)}{(\alpha +\beta )(\alpha +\beta +1)\cdots (\alpha +\beta +n-1)}}\end{aligned}}} para n ∈ N {\displaystyle n\in \mathbb {N} }
Función generadora de momentos La función generador de momentos de la variable aleatoria X {\displaystyle X}
M X ( t ) = ∑ n = 0 ∞ t n n ! B ( α + n , β ) B ( α , β ) = 1 + ∑ n = 1 ∞ ( ∏ r = 0 n − 1 α + r α + β + r ) t n n ! {\displaystyle {\begin{aligned}M_{X}(t)&=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}{\frac {\mathrm {B} (\alpha +n,\beta )}{\mathrm {B} (\alpha ,\beta )}}\\&=1+\sum _{n=1}^{\infty }\left(\prod _{r=0}^{n-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {t^{n}}{n!}}\end{aligned}}} Media geométrica El logaritmo de la media geométrica G X {\displaystyle G_{X}} variable aleatoria X {\displaystyle X} media aritmética de ln ( X ) {\displaystyle \ln(X)} valor esperado :
ln G X = E [ ln X ] {\displaystyle \ln G_{X}=\operatorname {E} [\ln X]} Para una distribución beta:
E [ ln X ] = ∫ 0 1 ln x f X ( x ) d x = ∫ 0 1 ln x x α − 1 ( 1 − x ) β − 1 B ( α , β ) d x = 1 B ( α , β ) ∫ 0 1 ∂ x α − 1 ( 1 − x ) β − 1 ∂ α d x = 1 B ( α , β ) ∂ ∂ α ∫ 0 1 x α − 1 ( 1 − x ) β − 1 d x = 1 B ( α , β ) ∂ B ( α , β ) ∂ α = ∂ ln B ( α , β ) ∂ α = ∂ ln Γ ( α ) ∂ α − ∂ ln Γ ( α + β ) ∂ α = ψ ( α ) − ψ ( α + β ) {\displaystyle {\begin{aligned}\operatorname {E} [\ln X]&=\int _{0}^{1}\ln xf_{X}(x)dx\\&=\int _{0}^{1}\ln x\;{\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}dx\\&={\frac {1}{\mathrm {B} (\alpha ,\beta )}}\int _{0}^{1}{\frac {\partial x^{\alpha -1}(1-x)^{\beta -1}}{\partial \alpha }}\;dx\\&={\frac {1}{\mathrm {B} (\alpha ,\beta )}}{\frac {\partial }{\partial \alpha }}\int _{0}^{1}x^{\alpha -1}(1-x)^{\beta -1}dx\\&={\frac {1}{\mathrm {B} (\alpha ,\beta )}}{\frac {\partial \mathrm {B} (\alpha ,\beta )}{\partial \alpha }}\\&={\frac {\partial \ln \mathrm {B} (\alpha ,\beta )}{\partial \alpha }}\\&={\frac {\partial \ln \Gamma (\alpha )}{\partial \alpha }}-{\frac {\partial \ln \Gamma (\alpha +\beta )}{\partial \alpha }}\\&=\psi (\alpha )-\psi (\alpha +\beta )\end{aligned}}} donde ψ {\displaystyle \psi } función digamma .
Distribuciones relacionadas Transformaciones Si X ∼ B ( α , β ) {\displaystyle X\sim \mathrm {B} (\alpha ,\beta )} 1 − X ∼ B ( β , α ) {\displaystyle 1-X\sim \mathrm {B} (\beta ,\alpha )} Si X ∼ B ( α , β ) {\displaystyle X\sim \mathrm {B} (\alpha ,\beta )} X 1 − X ∼ β ′ ( α , β ) {\displaystyle {\frac {X}{1-X}}\sim \beta '(\alpha ,\beta )} Si X ∼ B ( n 2 , m 2 ) {\displaystyle X\sim \mathrm {B} \left({\frac {n}{2}},{\frac {m}{2}}\right)} m X n ( 1 − X ) ∼ F n , m {\displaystyle {\frac {mX}{n(1-X)}}\sim F_{n,m}} Si X ∼ B ( α , 1 ) {\displaystyle X\sim \mathrm {B} (\alpha ,1)} − ln ( X ) ∼ Exponencial ( α ) {\displaystyle -\ln(X)\sim \operatorname {Exponencial} (\alpha )} Casos particulares Si X ∼ B ( 1 , 1 ) {\displaystyle X\sim \mathrm {B} (1,1)} X ∼ U ( 0 , 1 ) {\displaystyle X\sim \operatorname {U} (0,1)} lim n → ∞ n B ( 1 , n ) = Exponencial ( 1 ) {\displaystyle \lim _{n\to \infty }n\mathrm {B} (1,n)=\operatorname {Exponencial} (1)} lim n → ∞ n B ( k , n ) = Γ ( k , 1 ) {\displaystyle \lim _{n\to \infty }n\mathrm {B} (k,n)=\Gamma (k,1)} Un caso partícular de la Distribución Beta es la Distribución PERT que toma tres parámetros: Optimista, más frecuente y pesimista. Véase también Animación de la función de densidad de la distribución Beta para diferentes valores de sus parámetros
Control de autoridades Proyectos Wikimedia Q756254 Beta distribution / Q756254 Identificadores GND :4144975-7
Q756254 Beta distribution / Q756254 

 Datos: Q756254
Datos: Q756254 Multimedia: Beta distribution / Q756254
Multimedia: Beta distribution / Q756254





























![{\displaystyle {\text{E}}[X]={\frac {\alpha }{\alpha +\beta }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab8d12ff6bcad642fa716ef1dc34ae4d4dd01650)




![{\displaystyle {\begin{aligned}{\text{E}}[X^{n}]&={\frac {\mathrm {B} (\alpha +n,\beta )}{\mathrm {B} (\alpha +\beta )}}\\&=\prod _{r=0}^{n-1}{\frac {\alpha +r}{\alpha +\beta +r}}\\&={\frac {\alpha (\alpha +1)\cdots (\alpha +n-1)}{(\alpha +\beta )(\alpha +\beta +1)\cdots (\alpha +\beta +n-1)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f7119244b8e8f522b61b45f07dc0ce9054c7838)




![{\displaystyle \ln G_{X}=\operatorname {E} [\ln X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64b67cb73b90bc0e09ba41003b44f84b6e1d3feb)
![{\displaystyle {\begin{aligned}\operatorname {E} [\ln X]&=\int _{0}^{1}\ln xf_{X}(x)dx\\&=\int _{0}^{1}\ln x\;{\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}dx\\&={\frac {1}{\mathrm {B} (\alpha ,\beta )}}\int _{0}^{1}{\frac {\partial x^{\alpha -1}(1-x)^{\beta -1}}{\partial \alpha }}\;dx\\&={\frac {1}{\mathrm {B} (\alpha ,\beta )}}{\frac {\partial }{\partial \alpha }}\int _{0}^{1}x^{\alpha -1}(1-x)^{\beta -1}dx\\&={\frac {1}{\mathrm {B} (\alpha ,\beta )}}{\frac {\partial \mathrm {B} (\alpha ,\beta )}{\partial \alpha }}\\&={\frac {\partial \ln \mathrm {B} (\alpha ,\beta )}{\partial \alpha }}\\&={\frac {\partial \ln \Gamma (\alpha )}{\partial \alpha }}-{\frac {\partial \ln \Gamma (\alpha +\beta )}{\partial \alpha }}\\&=\psi (\alpha )-\psi (\alpha +\beta )\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad100ac91c363b10f11f43b63896a6c614ca0935)




















