Croix de Malte (mécanisme)

Pour le symbole chrétien, voir Croix de Malte (symbole). Pour les autres significations, voir Croix de Malte.
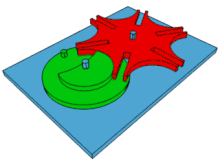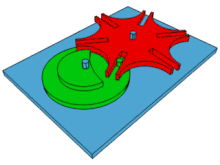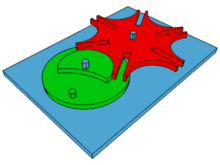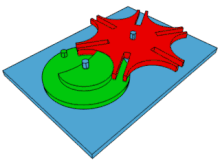
La croix de Malte est un dispositif mécanique permettant de transformer un mouvement de rotation continue en une rotation saccadée. Le dispositif mécanique consiste en une came entraînée par un « suiveur », permettant l'indexation.
Historique
L'inventeur Jules Carpentier en France, qui travaillait avec les frères Lumière, et Oskar Messter, l'un des pionniers du cinéma allemand, ont fait breveter des appareils à croix de Malte dès 1896. Mais c'est la croix de Malte à quatre branches de Pierre-Victor Continsouza qui fut ensuite la plus largement utilisée dans les appareils de projection cinématographique[1].
Etymologie
Le mecanisme doit son nom à sa ressemblance frappante avec la croix de Malte (✠, symbole de l'ordre de Saint-Jean de Jérusalem) nonobstant ses flancs concaves.
Dans les cultures anglo-saxonnes, à sensibilité généralement pragmatique et précis, le qualificatif maltais l'emporte: en anglais, Maltese cross, et en allemand, Malteserkreuzgetriebe — tandis que dans les pays d'influence latine, ce mécanisme prend le nom de la ville de Genève, haut lieu de developpements mécaniques: en anglais, Geneva drive, et en espagnol.
Utilisations
Il est notamment utilisé pour le cinéma argentique (non-numérique) dans les projecteurs et, rarement, dans des caméras, pour l'avance de la pellicule : la pellicule doit s'arrêter à chaque image devant l'obturateur (prise de vue) ou devant la lampe (projection).
On retrouve ce mécanisme dans les compteurs mécaniques (kilométrage automobile, consommation d'eau ou gaz, etc.) où il garantit l'alignement des chiffres et leur basculement à chaque retenue. Il est également utilisé dans des machines mettant en œuvre un transfert de produit avec la nécessité d'un temps d'attente au moment de l'introduction de celui-ci (ce que le système bielle-manivelle ne permet pas). Par exemple, on le retrouve à la base de mouvements utilisés sur des machines de conditionnement : les produits sont introduits dans un magasin d'alimentation suivant une quantité prédéfinie (phase d'arrêt), puis sont enveloppés pendant le mouvement de transfert (phase en mouvement).
Fonctionnement
Le fonctionnement du mécanisme à croix de Malte est le suivant : un cylindre, appelé manivelle ou roue menante, tourne de manière continue, avec une vitesse régulière, et porte un doigt. Le doigt pénètre dans une rainure de la croix de Malte (la roue menée), provoquant sa rotation de 1/n tour, où n est le nombre de rainures de la croix (n = 4 sur la figure ci-contre, 6 dans l'animation ci-dessus).
Puis, le doigt sort de la rainure, le cylindre moteur continue sa course tandis que la croix de Malte reste immobile. Le cylindre central, partiellement évidé, est complémentaire de l'arrondi de la croix de Malte ; ceci sert à stabiliser la position du dispositif lorsque le doigt n'est pas engagé dans une rainure.
Le nombre de rainures peut prendre des valeurs paires ou impaires, généralement entre 4 et 10.
Variantes
-
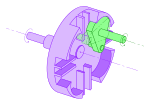 Croix de Malte interne.
Croix de Malte interne. -
 Fonctionnement d'une croix de Malte interne.
Fonctionnement d'une croix de Malte interne. -
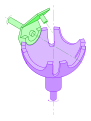 Croix de Malte sphérique.
Croix de Malte sphérique.
Il existe deux variantes : la croix de Malte interne, et la croix de Malte sphérique, « en tulipe » (système à axes concourants).
Dans le cas de la croix de Malte interne, l'axe moteur (portant la roue menante) est montée sur un arbre en porte-à-faux (en cantilever, il n'est tenu que d'un côté). L'arbre est donc plus sensible à la flexion, ce qui peut poser un problème si la charge est importante.
Par ailleurs, le temps d'entraînement est supérieur à une demi-période : il faut plus d'un demi-tour de roue menante pour faire tourner la roue menée d'un incrément. La durée d'entraînement (temps moteur) est donc supérieure à la durée de repos, contrairement à une croix de Malte externe. Par conséquent, l'accélération maximale est plus faible, mais présente toujours des discontinuités en début et fin de mouvement.
Dans le cas de la croix de Malte sphérique, l'arbre doit également être en porte-à-faux. Le temps d'entraînement est d'une demi-période ; la durée d'entraînement est égale à la durée de repos.
Hommages

Certains cinéastes ont rendu hommage à ce mécanisme, fondamental pour la prise de vue et la projection sur pellicule :
- Wim Wenders, dans L'Ami américain (1977) : un enfant, le fils de Jonathan et Marianne Zimmermann, joue avec une croix de Malte en bois ; et dans Au fil du temps (1976) « le cinéma n'existerait pas sans cette invention » d'après Bruno Winter personnage principal, réparateur de projecteurs.
- Martin Scorsese dans Hugo Cabret (2011) : lorsque Georges Méliès termine son automate, la dernière pièce qu'il met en place est une croix de Malte.
La croix de Malte était le logo de la marque de projecteurs Cinemeccanica (it). Le logo actuel ainsi que le logo de sa marque CineCloud sont une croix de Malte stylisée (voir le logo sur la page officielle).
Étude mécanique
Contraintes géométriques

Le point critique du fonctionnement est le moment où le doigt entre dans la rainure. Cela impose une relation entre le rayon de la manivelle R, c'est-à-dire la distance entre le centre du doigt et le centre de la roue menante qui le supporte, et l'entraxe E, c'est-à-dire la distance entre le centre de la roue menante et le centre de la croix de Malte. Pour qu'il n'y ait pas de choc, le vecteur vitesse doit être dans l'axe de la rainure.
On appelle α la moitié de l'angle de rotation de la roue menée par tour de roue menante
- en radians
soit α = π/4 = 45° pour quatre rainures, et α = π/6 = 30° pour six rainures. On a alors les relations suivantes entre l'entraxe E, le rayon de la roue menante R1 et le rayon de la roue menée R2 :
Entre 0 et π/4 (0 et 90°), la fonction sinus est croissante et la fonction cosinus est décroissante en α. On en déduit que pour un entraxe donne, plus on a de rainures (plus n est grand), plus α est petit donc plus R1 est petit et plus R2 est grand.
Représentons le système au moment où le doigt pénètre dans la rainure. Nous plaçons la droite reliant les centres des roue à l'horizontale. La rainure fait donc un angle α avec l'horizontale Le vecteur vitesse est perpendiculaire à la trajectoire ; comme le doigt décrit un cercle, la droite portant le vecteur vitesse est donc tangente au cercle, c'est-à-dire perpendiculaire au rayon en ce point. Nous avons donc un triangle rectangle d'hypoténuse E, dont l'un des angles vaut π/n et dont le côté opposé à l'angle a pour longueur R1. Nous avons donc :
Le rayon du cercle circonscrit à la croix de Malte est par ailleurs la longueur du côté adjacent du triangle rectangle, soit
Par ailleurs, la largeur nominale de la rainure doit être égale au diamètre nominal 2r du doigt : plus petite, le doigt ne pourrait pas entrer, trop grande, il y aurait un choc. Dans la pratique, il existe un jeu : la rainure doit être légèrement plus large que le doigt pour permettre le mouvement. On peut utiliser un ajustement dit « glissant sans jeu », ou plus précisément « guidage précis », noté H7/g6, pour limiter les chocs, mas celui-ci coûte cher à réaliser.

L'extrémité des branches doit avoir une largeur non nulle. Il faut de fait imposer une largeur minimale e1, qui dépend de la résistance souhaitée. Cela impose un rayon maximum pour le cylindre immobilisateur. Par ailleurs, le contact doit être effectif, il y a donc un rayon minimum, soit :
la dimension e1 étant l'épaisseur que l'on désire garder en bout de branche pour avoir une résistance suffisante.
On a en cote nominale (en supposant un jeu nul) :
soit
Du fait du jeu nécessaire, il faut en fait
la différence (R1 - r - e1) - R3 étant le jeu.
Le contact doit être effectif, on a donc également nécessairement :
soit
- .

La longueur minimale de la rainure L s'obtient en considérant la position pour laquelle le doigt est le plus engagé. On a alors, en orientant les longueurs vers la gauche :
La longueur maximale est celle laissant suffisamment de matière pour que la croix de Malte résiste aux contraintes. Si l'on appelle ra le rayon de l'arbre de la croix de Malte et e2 l'épaisseur minimale de matière que l'on veut, alors on a :
Étude cinématique

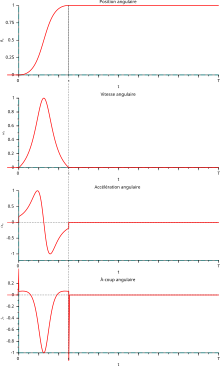
On suppose que la roue menante (manivelle) tourne avec une vitesse angulaire ω constante (mouvement de rotation uniforme). La figure ci-contre représente le mécanisme en cours de fonctionnement. Si l'on note comme précédemment
- n le nombre de rainures que comporte la croix de Malte (roue menée) ;
- α = 2π/n l'angle entre deux rainures
et que l'on introduit le rapport
alors on relève que :
- la vitesse angulaire maximale de la roue menée vaut
; - l'accélération angulaire maximale vaut, selon le nombre de rainures :
- n = 4 : α0 ≃ 3,82 × ω2,
- n = 6 : α0 ≃ 0,375 × ω2,
- n = 8 : α0 ≃ 0,268 × ω2 ;
- l'accélération angulaire initiale et finale ne sont pas nulles, ce qui signifie que la roue menée subit des à-coups angulaires infinis (diracs), dans la pratique limités par l'élasticité et les frottements du système.
Ces pics d'à-coup ne posent pas de problème tant que l'on reste dans des vitesses et des inerties faibles. Ils deviennent par contre rédhibitoires pour des systèmes à haute cadence et à forte charges.
On appelle angle d'entrée, et on note θe, l'angle que fait le rayon passant par le doigt avec l'axe des x, et qui caractérise l'orientation de la roue menante. On appelle angle de sortie, et on note θs, l'angle que fait l'axe d'une rainure par rapport à l'axe des x, et qui caractérise l'orientation de la roue menée.
Étude de l’intermittence
L'angle d'entrée θe évolue de manière uniforme
la vitesse angulaire ω est négative sur le dessin. L'équation horaire de l'angle d'entrée s'écrit donc
où φ est l'angle à t = 0, choisi arbitrairement. Pour la représentation graphique, nous choisissons φ de sorte que le doigt entre dans la rainure à t = 0, soit
- .
La durée d'entraînement τ correspond à une rotation de la roue menante d'un angle φ à l'angle symétrique -φ, soit
soit
La période totale vaut T = -2π/ω, donc la phase d'entraînement est une fraction de la période totale valant
Par la suite, pour des raisons de simplicité, nous déterminons θs en fonction de θe plutôt que de t.
Étude des relations angulaires
L'angle d'entrée est relié à l'angle de sortie par le fait que les deux triangles rectangles ont le même côté opposé h :
On a donc
soit
Lois de mouvement
En préliminaire, calculons les dérivées suivantes :
et de la même manière
On obtient la vitesse angulaire de la roue menée par dérivation. Reprenons l'expression de tan θs. Si l'on dérive le membre de gauche, on a
soit
et en dérivant le membre de droite :
En écrivant l'égalité des deux membres, on obtient
En dérivant, on détermine l'accélération angulaire :
- .
On note que cette accélération s'annule pour θe = 0, donc la vitesse est maximale en ce point, est
- .
À l'origine, on a θe = φ et donc
on a donc un à-coup infini à l'origine. Par symétrie, on a un à-coup infini à la fin du mouvement.
En dérivant l'accélération, on obtient l'à-coup en cours de mouvement :
L'accélération est maximale lorsque l'à-coup s'annule, ce qui revient à résoudre :
soit, en posant x = cos θe
qui est une équation du second degré de discriminant strictement positif
L'équation admet donc deux solutions réelles
On obtient, pour quelques valeurs de n :
| n | k | x1 | x2 | θe | Acc. max. |
|---|---|---|---|---|---|
| 4 | √2 | 0,980 | 1,33 | -0,200 rad (-11,5°) | 3,82 × ω2 |
| 6 | 2 | 0,921 | 1,17 | -0,400 rad (-22,9°) | 0,675 × ω2 |
| 8 | 2,61 | 0,851 | 1,04 | -0,552 rad (-31,6 °) | 0,268 × ω2 |
Application numérique
Considérons un projecteur de cinéma muni d'une croix de Malte à quatre rainures. Nous avons donc :
- une fréquence de rotation de la roue menante N = 24 Hz (24 images par seconde), soit ω = 2πN ≃ 151 rad/s ;
- un rapport valant k = 1/sin(π/4) = √2 ≃ 1,41 ;
et donc
- ω0 ≃ 364 rad/s ; N0 = 57,9 tr/s ;
- α0 ≃ 8,69 × 104 rad/s2.
Notes et références
- ↑ « Croix de Malte », sur projecteur.mip.free.fr (consulté le )
Voir aussi
Sur les autres projets Wikimedia :
- Le mécanisme de la croix de Malte, sur Wikimedia Commons
Bibliographie
- (en) John H. Bickford, Mechanisms for intermittent motion, New York, Industrial Press inc., , 264 p. (ISBN 0-8311-1091-0, lire en ligne), chap. 9 (« Geneva Mechanisms »), p. 127-138
Articles connexes
Liens externes
- La croix de Malte sur le site de l'université de Nantes (animation en cabri Java)
- La croix de Malte : site relatif aux débuts de l'Histoire du cinéma vus à travers les livres d'époque
 Portail du génie mécanique
Portail du génie mécanique  Portail de la réalisation audiovisuelle
Portail de la réalisation audiovisuelle  Portail du cinéma
Portail du cinéma




















































