Graphe biparti

En théorie des graphes, un graphe est dit biparti si son ensemble de sommets peut être divisé en deux sous-ensembles disjoints $U$ et $V$ tels que chaque arête ait une extrémité dans $U$ et l'autre dans $V$ .

Un graphe biparti permet notamment de représenter une relation binaire.

Caractérisation

Il existe plusieurs façons de caractériser un graphe biparti.

Par le nombre chromatique: Les graphes bipartis sont les graphes dont le nombre chromatique est inférieur ou égal à 2.

Par la longueur des cycles: Un graphe est biparti si et seulement s'il ne contient pas de cycle impair^[1].

Démonstration

Supposons qu'un graphe est décomposé en deux partitions $U$ et $V$ telles que toute arête relie un sommet de $U$ à un sommet de $V$ . Considérons un cycle quelconque. Ce cycle passe alternativement par les deux parties $U$ et $V$ avant de rejoindre le sommet de départ et a donc une longueur paire.

{\displaystyle r} — Construction des deux partitions dans un graphe ne comportant que des cycles de longueur paire : l'arbre couvrant est en rouge, on colore les sommets en bleu et blanc alternativement depuis sa racine $r$ .

La réciproque est quelque peu plus dure à démontrer. Supposons que l'on ait un graphe $G$ qui ne comporte que des cycles de longueur paire. Pour simplifier, supposons également que $G$ est connexe (si jamais il ne l'était pas, on pourrait raisonner individuellement sur chaque composante connexe).

Comme $G$ est connexe, il possède un arbre couvrant $T$ . Notons $r$ une racine de cet arbre. Créons deux ensembles de sommets $U$ et $V$ de la manière suivante :

$U$ contient $r$ et tous les sommets de $T$ se trouvant à un nombre pair d'arêtes de $r$ ;
$V$ contient les sommets de $T$ se trouvant à un nombre impair d'arêtes de $r$ .

Les ensembles de sommets $U$ et $V$ sont disjoints et contiennent tous les sommets de $G$ . Cela ne suffit cependant pas à montrer que $G$ est biparti : en effet, rien ne garantit a priori que l'on n'ait pas une arête « en trop » de $G$ qui relie deux sommets de $U$ , par exemple.

Considérons deux sommets $x$ et $y$ de $G$ dans une même partie ( $U$ ou $V$ ) et reliés par une arête $e$ . Le chemin qui relie $x$ à $y$ dans $T$ est forcément de longueur paire, par construction de $U$ et de $V$ . Si l'on ajoute l'arête $e$ , on obtient un cycle de longueur impaire, ce qui est interdit par hypothèse.

Il n'est donc pas possible d'avoir de tels sommets $x$ et $y$ reliés en « court-circuit ». Toutes les arêtes du graphe relient des sommets de $U$ à des sommets de $V$ , ce qui achève de montrer que $G$ est biparti.

Par le spectre: Si un graphe est biparti, alors son spectre vérifie la propriété suivante^[2] :

\lambda

est une valeur propre de la matrice d'adjacence du graphe, alors

-\lambda

en est aussi une, avec la même multiplicité que celle de

\lambda

Par les polyèdres: Un graphe est biparti si et seulement si son polytope des stables est décrit par les contraintes de clique de taille 2.

Graphes bipartis particuliers

Les graphes suivants sont bipartis : le graphe vide, les arbres, les cycles de longueurs paires, les hypercubes et les grilles.

De plus, on définit les graphes bipartis suivants :

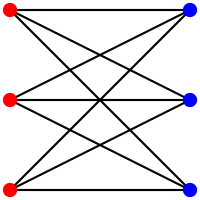
Un graphe biparti est dit biparti complet (ou encore est appelé une biclique) si chaque sommet de $U$ est relié à chaque sommet de $V$ .
Un graphe biparti est dit birégulier si tous les sommets de $U$ ont le même degré, et si tous les sommets de $V$ ont le même degré.
Les graphes bipartis de Kneser sont une famille de graphes bipartis permettant de décrire des relations d'inclusion entre ensembles.
110-graphe de Iofinova-Ivanov

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Bipartite graph » (voir la liste des auteurs).

↑ (en) Armen S. Asratian, Tristan M. J. Denley et Roland Häggkvist, « Bipartite Graphs and their Applications », Cambridge Tracts in Mathematics, Cambridge University Press, vol. 131,‎ 1998 (ISBN 9780521593458), Théorème 2.1.3, p. 8. Les auteurs attribuent cette caractérisation à Dénes Kőnig dans un article de 1916.
↑ (en) Norman Biggs, Algebraic Graph Theory, Cambridge University Press, 1994, 2^e éd., 205 p. (ISBN 978-0-521-45897-9, lire en ligne), p. 53.