Logarithme binaire

Cet article est une ébauche concernant l’analyse.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

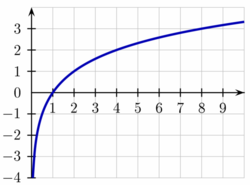
En mathématiques, le logarithme binaire (log₂ n) est le logarithme de base 2. C’est la fonction réciproque de la fonction puissance de deux : x ↦ 2^x. Le logarithme binaire de x est la puissance à laquelle le nombre 2 doit être élevé pour obtenir la valeur x, soit : ${\displaystyle \operatorname {lb} (x)=a\Leftrightarrow x=2^{a}}$.

Ainsi, le logarithme binaire de 1 est 0, le logarithme binaire de 2 est 1, le logarithme binaire de 4 est 2, le logarithme binaire de 8 est 3.

On le notait^[Quand ?] ld () (pour logarithmus dualis), mais la norme ISO 80000-2^[1] indique que log₂(x) devrait être symbolisé par lb (x). En fait, en analyse de la complexité des algorithmes, dans un contexte dans lequel il n'y a pas de confusion possible, il est parfois simplement noté log (x)^[2].

Musique

En musique, le logarithme binaire intervient dans la formule permettant de déterminer la valeur en cents d’un intervalle. Cette valeur est égale en cents à 1200 fois le logarithme binaire du rapport de fréquence de l'intervalle. Le rapport de fréquence d'un intervalle est le quotient de la fréquence la plus haute sur la fréquence la plus basse de cet intervalle. Un cent vaut exactement un centième de demi-ton.

Informatique

En informatique, l'orientation binaire du matériel fait souvent du logarithme binaire le plus facile à calculer et le plus précis, les autres en étant dérivés.

En effet, soit (e ; m) la représentation virgule flottante binaire d'un nombre réel non nul x, où e est un entier porteur de l'ordre de grandeur, et m un significande tel que 1 ≤ |m| < 2. Alors, si m > 0 :

${\displaystyle x=m\times 2^{e}\ {\textrm {entraine}}\ \operatorname {lb} (x)=e+\operatorname {lb} (m).}$

et le calcul de lb(x) se ramène ainsi au domaine [1 ; 2[

Par exemple, 10 = 2³ × 1,25, lb(10)= 3 + lb(1,25).

où lb(1,25) est la partie fractionnaire du logarithme cherché.

Chaque bit de lb(1,25) peut se calculer directement bit à bit à l'aide des relations :

${\displaystyle \operatorname {lb} (1)=0;\operatorname {lb} (x)=\operatorname {lb} (x^{2})/2;\operatorname {lb} (x)=\operatorname {lb} (x/2)+1.}$

Quand on cherche un nouveau bit de x (0 < x < 2) :

• on élève x au carré
  • si x vaut au moins 2, on note 1, on divise x par 2 et on poursuit ;
  • sinon, on note 0 et on poursuit^[3].

Ainsi

${\displaystyle {\begin{aligned}\operatorname {lb} (10)&=11_{2}+\operatorname {lb} (1,25)=11_{2}+\operatorname {lb} (1,5625)/2\\&=11,0_{2}+\operatorname {lb} (2,44140625)/4=11,01_{2}+\operatorname {lb} (1,220703125)/4\\&=11,01_{2}+\operatorname {lb} (1,490116119)/8=11,010_{2}+\operatorname {lb} (2,220446049)/16\\&=11,0101_{2}+\operatorname {lb} (1,110223025)/16=11,01010_{2}+\operatorname {lb} (1,232611)/32=11,010100_{2}+\operatorname {lb} (1,519330)/64=11,010100_{2}+\operatorname {lb} (2,308)/128.....\end{aligned}}}$

Or 11,0101001₂ = 3,3203125, et on a déjà 2^3,3203125 = 9,9888...

Remarque

La valeur lb(10) = 3,32... entraîne que le codage binaire d'un entier décimal occupera au moins 3,32 bits par chiffre décimal, soit 4 bits pour un chiffre, 7 bits pour 2 chiffres et 10 bits pour 3 chiffres (ou tranche de 3 chiffres).

Références

Voir aussi

• Cologarithme
• Logarithme, symbole normalisé log
• Logarithme naturel (base e), symbole normalisé ln
• Logarithme décimal (base 10), symbole normalisé lg
• Virgule flottante

• Portail de l'analyse