ドラゴン曲線

ドラゴン曲線（ドラゴンきょくせん、英語: Dragon curve）とは、L-system（リンデンマイヤー・システム）のような再帰法を用いて構成することの出来る、ある自己相似性フラクタルの族に含まれている曲線のことを言う。

ヘイウェイ・ドラゴン

ヘイウェイ・ドラゴン（ハーター・ヘイウェイ・ドラゴンあるいはジュラシック・パーク・ドラゴンとも呼ばれる）は、NASAの物理学者のジョン・ヘイウェイ、ブルース・バンクスおよびウィリアム・ハーターによって初めて研究され、1967年、雑誌『サイエンティフィック・アメリカン（Scientific American）』のマーティン・ガードナーによるコラム「数学ゲーム（Mathematical Games」で紹介された。その性質についてはチャンドラー・デイビスとドナルド・クヌースによって初めて出版化された。マイケル・クライトンの小説『ジュラシック・パーク』の節ごとのタイトルページで使用されている。

構成方法

ヘイウェイ・ドラゴンは、

• 角度 90°
• 初期文字列 FX
• 文字列書き換え規則
  • X ${\displaystyle \rightarrow }$ X+YF+
  • Y ${\displaystyle \rightarrow }$ −FX−Y.

であるようなL-systemにより構成することが出来る。

また、次のような手順で描くことが出来る: 基本となる線分から始めて、各線分を「直角をなすような二つの線分」によって置き換える。ただし置き換える際に線分を回転させる方向は、右、左…と交互になるようにする。

ヘイウェイ・ドラゴンは次のような複素平面における反復関数系の極限集合でもある:

${\displaystyle f_{1}(z)={\frac {\left(1+i\right)z}{2}}}$

${\displaystyle f_{2}(z)=1-{\frac {\left(1-i\right)z}{2}}}$

ここで、点の初期集合は ${\displaystyle S_{0}=\{0,1\}}$ とする。

実数のペアを用いれば、これは次のような二つの関数

${\displaystyle f_{1}(x,y)={\frac {1}{\sqrt {2}}}{\begin{bmatrix}\cos 45^{\circ }&-\sin 45^{\circ }\\\sin 45^{\circ }&\cos 45^{\circ }\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}\equiv {\dfrac {1}{2}}{\begin{bmatrix}1&-1\\1&1\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}},}$

${\displaystyle f_{2}(x,y)={\frac {1}{\sqrt {2}}}{\begin{bmatrix}\cos 135^{\circ }&-\sin 135^{\circ }\\\sin 135^{\circ }&\cos 135^{\circ }\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}+{\begin{bmatrix}1\\0\end{bmatrix}}\equiv {\dfrac {1}{2}}{\begin{bmatrix}-1&-1\\1&-1\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}+{\begin{bmatrix}1\\0\end{bmatrix}}}$

とも等しい。Apophysisのようなソフトウェアでは、こちらの表現の方が一般的に使われている。

次元

• その奇妙な外観にかかわらず、ヘイウェイ・ドラゴン曲線の次元は単純なものである。

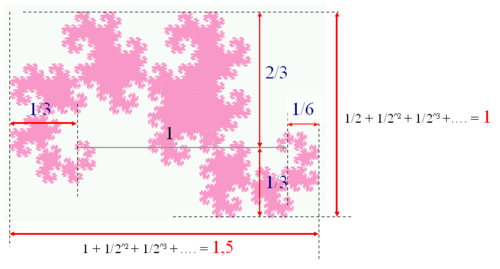
• その表面（surface）も単純である。初期線分が 1 と等しいなら、その表面は ${\displaystyle \textstyle {\frac {1}{2}}}$ と等しくなる。この結果は、曲線が敷き詰められていく性質に起因する。
• その境界の長さは無限大である。なぜならば、反復が行われる毎に係数 ${\displaystyle {\sqrt {2}}}$ によって増大していくからである^[1]。
• ヘイウェイ・ドラゴン曲線は、自分自身とは決して交わらない。
• ヘイウェイ・ドラゴン曲線には多くの自己相似性が見られる。もっとも分かりやすいものは、45° の傾きと減少率 ${\displaystyle \textstyle {\sqrt {2}}}$ を伴うパターンの繰り返しである。

• そのフラクタル次元は計算によって ${\displaystyle \textstyle {{\frac {\ln 2}{\ln {\sqrt {2}}}}=2}}$ であることが分かる。これにより、ヘイウェイ・ドラゴン曲線は空間充填曲線であることが分かる。

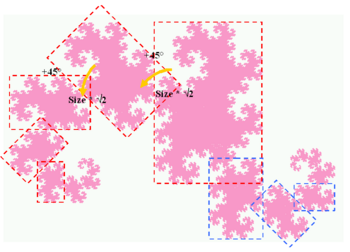
• その境界のフラクタル次元の数値的な近似は Chang と Zhang によって得られた^[2]。実際、解析的には

${\displaystyle \log _{2}{\frac {1+{\sqrt[{3}]{73-6{\sqrt {87}}}}+{\sqrt[{3}]{73+6{\sqrt {87}}}}}{3}}\cong 1.523627086202492.}$

と得られる^[3]。これは方程式 ${\displaystyle \textstyle {4^{x}\left(2^{x}-1\right)=4\left(2^{x}+1\right)}}$ の根である。

タイル張り

ドラゴン曲線には、平面上にタイル張りする方法が多く存在する。

ツインドラゴン

二つのヘイウェイ・ドラゴンを背中合わせに配置することにより、ツインドラゴン（デイビス-クヌース・ドラゴンとも呼ばれる）を作ることが出来る。それは反復関数系

${\displaystyle f_{1}(z)={\frac {(1+i)z}{2}}}$

${\displaystyle f_{2}(z)=1-{\frac {(1+i)z}{2}}}$

の極限集合でもある。ここでの初期形状は集合 ${\displaystyle S_{0}=\{0,1,1-i\}}$ により定義される。

テルドラゴン

テルドラゴンはL-system

• 角度 120°
• 初期文字列 F
• 文字列書き換え規則
  • F ${\displaystyle \rightarrow }$ F+F−F.

により書くことが出来る。それは反復関数系

${\displaystyle f_{1}(z)=\lambda z}$

${\displaystyle f_{2}(z)={\frac {i}{\sqrt {3}}}z+\lambda }$

${\displaystyle f_{3}(z)=\lambda z+\lambda ^{*}}$

の極限集合でもある。ただし ${\displaystyle \lambda ={\frac {1}{2}}-{\frac {i}{2{\sqrt {3}}}}}$ および ${\displaystyle \lambda ^{*}={\frac {1}{2}}+{\frac {i}{2{\sqrt {3}}}}}$ である。

レヴィ・ドラゴン

レヴィC曲線はしばしばレヴィ・ドラゴンとも呼ばれる。

解集合から導かれるドラゴン曲線

ある微分方程式の解集合が得られたとき、それらの解の線形結合は、重ね合わせの原理により再び元の微分方程式を満たすものとなる。これはすなわち、すでに存在している解の集合に対してある関数を適用することによって、新たな解を導くことが出来るという意味でもある。これは反復関数系を用いてある集合内に新たな点を導出する方法と同様である（ただし、そのような反復関数は線形関数であるとは限らない）。同様な概念により、関数の集合へとそのような反復的な手法を用いることによって、リトルウッド多項式（英語版）の集合を導くことが出来る。

リトルウッド多項式とは、多項式

${\displaystyle p(x)=\sum _{i=0}^{n}a_{i}x^{i}\,}$

のことである（ここで ${\displaystyle a_{i}}$ は 1 か -1 のいずれか）。

|w| < 1 を満たすようなある w に対して、関数系

${\displaystyle f_{+}(z)=1+wz}$

${\displaystyle f_{-}(z)=1-wz}$

を定義する。どのような次数 d のリトルウッド多項式であっても、この関数系の z=0 から始めた d+1 回の反復操作によって導出することが出来る^[4]。例えば、${\displaystyle f_{+}(f_{-}(f_{-}(0)))=1+(1-w)w=1+1w-1w^{2}}$ など。

w = (1+i)/2 である場合、上の関数系はヘイウェイ・ドラゴンの反復関数系と等しいことが分かる。すなわち、ヘイウェイ・ドラゴンは、ある反復操作によって、点 w = (1+i)/2 において評価されるある次数までのすべてのリトルウッド多項式からなる集合を表すものである。実際、リトルウッド多項式の根を十分多くの数プロットしたとき、それらの座標の近くにドラゴン曲線と似た構造が現れることとなる^[4][5][6]。

注釈

1. ^ http://library.thinkquest.org/26242/full/fm/fm8.html
2. ^ Fractal dimension of the boundary of the Dragon curve
3. ^ "The Boundary of Periodic Iterated Function Systems" by Jarek Duda, The Wolfram Demonstrations Project. Recurrent construction of the boundary of dragon curve.
4. ^ ^{a b} http://golem.ph.utexas.edu/category/2009/12/this_weeks_finds_in_mathematic_46.html
5. ^ http://math.ucr.edu/home/baez/week285.html
6. ^ http://johncarlosbaez.wordpress.com/2011/12/11/the-beauty-of-roots/

参考文献

• Donald Knuth, The Art of Computer Programming, vol. 2. Addison-Wesley.

関連項目

• ドラゴン
• ハウスドルフ次元によるフラクタルの一覧（英語版）
• 複素基本系（英語版）
• 正規折紙列（英語版）

外部リンク

ウィキメディア・コモンズには、ドラゴン曲線に関連するメディアがあります。

• Dragon Curve—from MathWorld
• Dragon Curve Maker in Flash
• Tile made by David Chow
• Twin dragon tile with JAVA
• Crochet representation of Dragon Curves

表 話 編 歴 フラクタル
特徴	フラクタル次元 Assouad（英語版） Box-counting（英語版） Correlation（英語版） ハウスドルフ Packing（英語版） 位相 再帰（英語版） 自己相似 自己相似過程 スケール不変性
反復関数系	バーンズリーのシダ カントール集合 ドラゴン曲線 レヴィC曲線 コッホ雪片 メンガーのスポンジ シェルピンスキーのカーペット シェルピンスキーの三角形 空間充填曲線 T-square（英語版）
ストレンジアトラクター	多重フラクタル系（英語版）
L-system	空間充填曲線
Escape-time fractals	バーニングシップ・フラクタル ジュリア集合 充填 リアプノフ・フラクタル マンデルブロ集合 ニュートン・フラクタル（英語版）
確率的フラクタル	ブラウン運動 非整数ブラウン運動 ブラウンの木（英語版） 拡散律速凝集 フラクタル地形 Lévy flight（英語版） パーコレーション理論（英語版） Self-avoiding walk（英語版）
人物	ゲオルク・カントール フェリックス・ハウスドルフ ガストン・ジュリア ヘルゲ・フォン・コッホ ポール・レヴィ アレクサンドル・リャプノフ ブノワ・マンデルブロ ルイス・フライ・リチャードソン ヴァツワフ・シェルピニスキ
その他	"How Long Is the Coast of Britain?（英語版）" 海岸線のパラドックス List of fractals by Hausdorff dimension（英語版） The Beauty of Fractals（英語版） (1986 book)
カテゴリ