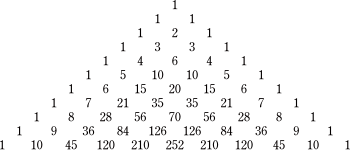三角錐数

三角錐数（さんかくすいすう、triangular pyramidal number）は球を右図のように三角錐の形にならべたとき、そこに含まれる球の総数にあたる自然数である。つまり三角数を1から小さい順に足した数のことである。四面体数（しめんたいすう、tetrahedral number）ともいう。

例： 1, 4 (=1+3), 10 (=1+3+6), 20 (=1+3+6+10), 35 (=1+3+6+10+15)

n 番目の三角錐数 T_n は1から n 番目の三角数 n(n + 1)/2 までの和に等しいので

${\displaystyle {\begin{aligned}T_{n}=\sum _{k=1}^{n}{\frac {k(k+1)}{2}}&={\frac {1}{2}}\left({\frac {n(n+1)(2n+1)}{6}}+{\frac {n(n+1)}{2}}\right)\\&={\frac {n(n+1)(n+2)}{6}}\\\end{aligned}}}$

また組み合わせの記号を用いると ${\displaystyle T_{n}={}_{n+2}{\rm {C}}_{3}\,}$ となる。

三角錐数を小さい順に列記すると

1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969, …（オンライン整数列大辞典の数列 A292）。

性質

• 三角錐数のうち平方数でもある数は 1, 4 と 19600 (=140²) の3つのみである。(オンライン整数列大辞典の数列 A003556)

• 三角錐数でなおかつ四角錐数でもある数は 1 のみである。

• 三角錐数のうち三角数でもある数は1, 10, 120, 1540, 7140 の5つのみである。（オンライン整数列大辞典の数列 A027568）

• 2つの連続する三角錐数の和は四角錐数になる。

• 三角錐数の奇数番目は奇数の平方和、偶数番目は偶数の平方和で表される。(例.35=1²+3²+5²、56=2²+4²+6²)

奇数の時　${\displaystyle \sum _{k=1}^{n}(2k-1)^{2}={\frac {(2n-1)\cdot 2n\cdot (2n+1)}{6}}}$

偶数の時　${\displaystyle \sum _{k=1}^{n}(2k)^{2}={\frac {2n(2n+1)(2n+2)}{6}}}$

• 三角錐数は奇数-偶数-偶数-偶数といった順番の繰り返しで現れる。

(奇数…オンライン整数列大辞典の数列 A015219、偶数…オンライン整数列大辞典の数列 A015220)

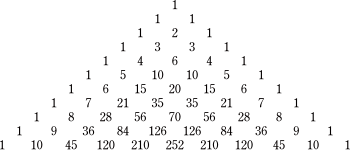• パスカルの三角形における数列は左上（または右上）にある列から順に

モナド(単数)の数列　1, 1, 1, 1, 1, 1, 1, 1, 1,…, ${\displaystyle {}_{n-1}{\rm {C}}_{0}\,}$,…

自然数の数列　1, 2, 3, 4, 5, 6, 7, 8, 9,…, ${\displaystyle {}_{n}{\rm {C}}_{1}\,}$ ,…

三角数の数列　1, 3, 6, 10, 15, 21, 28, 36, 45,…, ${\displaystyle {}_{n+1}{\rm {C}}_{2}\,}$ ,…

三角錐数の数列　1, 4, 10, 20, 35, 56, 84, 120, 165,…, ${\displaystyle {}_{n+2}{\rm {C}}_{3}\,}$ ,…

となっている。左上（または右上）にある数列はその一つ右下（または左下）の数列の階差数列である。

• 三角錐数の逆数の総和は

${\displaystyle {\begin{aligned}\sum _{k=1}^{\infty }{\frac {1}{\frac {k(k+1)(k+2)}{6}}}&=6\sum _{k=1}^{\infty }{\frac {1}{2}}\left({\frac {1}{k}}-{\frac {2}{k+1}}+{\frac {1}{k+2}}\right)\\&=3{\bigg \{}\left({\frac {\color {Green}\not 1}{\color {Green}\not 1}}-{\frac {\color {Green}\not 2}{\color {Green}\not 2}}+{\frac {\not 1}{\not 3}}\right)+\left({\frac {1}{2}}-{\frac {\not 2}{\not 3}}+{\frac {\color {Red}\not 1}{\color {Red}\not 4}}\right)+\left({\frac {\not 1}{\not 3}}-{\frac {\color {Red}\not 2}{\color {Red}\not 4}}+{\frac {1}{5}}\right)+\left({\frac {\color {Red}\not 1}{\color {Red}\not 4}}-{\frac {2}{5}}+{\frac {1}{6}}\right)+\cdots {\bigg \}}\\&={\frac {3}{2}}\end{aligned}}}$

関連項目

プロジェクト 数学

ポータル 数学

• 図形数
• 三角数
• 三角錐
• 球充填
• 四角錐数, 五角錐数

外部リンク

• Weisstein, Eric W. "Tetrahedral Number". mathworld.wolfram.com (英語).