位相空間

定義 (開集合系による位相空間の定義) ―  Xを集合とし、${\displaystyle {\mathcal {O}}}$をXのべき集合${\displaystyle {\mathfrak {P}}(X)}$の部分集合とする。

${\displaystyle {\mathcal {O}}}$が以下の性質を満たすとき、組 ${\displaystyle (X,{\mathcal {O}})}$ を X を台集合とし${\displaystyle {\mathcal {O}}}$を開集合系とする位相空間と呼び、${\displaystyle {\mathcal {O}}}$の元を X の開集合と呼ぶ。

1. ${\displaystyle \emptyset ,\,X\in {\mathcal {O}}}$
2. ${\displaystyle \forall O_{1},\forall O_{2}\in {\mathcal {O}}~:~O_{1}\cap O_{2}\in {\mathcal {O}}}$
3. ${\displaystyle \forall \{O_{\lambda }\}_{\lambda \in \Lambda }\subset {\mathcal {O}}~:~\bigcup _{\lambda \in \Lambda }O_{\lambda }\in {\mathcal {O}}}$

定義 (閉集合系による位相空間の定義) ―  Xを集合とし、${\displaystyle {\mathcal {F}}}$をXのべき集合${\displaystyle {\mathfrak {P}}(X)}$の部分集合とする。

${\displaystyle {\mathcal {F}}}$が以下の性質を満たすとき、組 ${\displaystyle (X,{\mathcal {F}})}$ を X を台集合とし${\displaystyle {\mathcal {F}}}$を閉集合系とする位相空間と呼び、${\displaystyle {\mathcal {F}}}$の元を X の閉集合と呼ぶ。

1. ${\displaystyle \emptyset ,X\in {\mathcal {F}}}$
2. ${\displaystyle \forall F_{1},\forall F_{2}\in {\mathcal {F}}~~:~~F_{1}\cup F_{2}\in {\mathcal {F}}}$
3. ${\displaystyle \forall \{F_{\lambda }\}_{\lambda \in \Lambda }\subset {\mathcal {F}}~~:~~\bigcap _{\lambda \in \Lambda }F_{\lambda }\in {\mathcal {F}}}$

定義 (位相同型) ―  ある全単射

${\displaystyle f~:~X\to Y}$

が存在して、

${\displaystyle O\in {\mathcal {O}}_{X}\iff f(O)\in {\mathcal {O}}_{Y}}$

を満たすとき、${\displaystyle (X,{\mathcal {O}}_{X})}$と${\displaystyle (Y,{\mathcal {O}}_{Y})}$は位相同型であるという。

定理・定義 (距離から定まる位相) ―  (X ,d )を距離空間とし、実数 ε > 0 と x ∈ X に対し、xのε-近傍（ε-neighborhood）${\displaystyle B_{\varepsilon }(x)}$を

${\displaystyle B_{\varepsilon }(x):=\{y\in X\mid d(x,y)<\varepsilon \}}$

と定義するとき、

${\displaystyle {\mathcal {O}}_{d}=\{O\subset X\mid \forall x\in O\exists \varepsilon >0~~:~~B_{\varepsilon }(x)\subset O\}}$

は開集合系の公理を満たす。 ${\displaystyle {\mathcal {O}}_{d}}$を距離 d により定まる X の開集合系、もしくはd により定まる X の位相構造といい、 ${\displaystyle (X,{\mathcal {O}}_{d})}$を(X ,d )により定まる位相空間という。

命題 (距離から定まる開集合の特徴づけ) ― 距離空間(X ,d )が定める位相を${\displaystyle {\mathcal {O}}_{d}}$とし、OをXの部分集合とする。このとき、以下の３条件は同値である：

1. Oは${\displaystyle {\mathcal {O}}_{d}}$の開集合である
2. 任意のx ∈ Oに対し、ある${\displaystyle \varepsilon _{x}>0}$が存在し、${\displaystyle O=\bigcup _{x\in O}B_{\varepsilon _{x}}(x)}$が成立する。
3. Oは（有限または無限個の）開球の和集合として書ける。すなわち族${\displaystyle \{B_{\varepsilon _{\lambda }}(x_{\lambda })\}_{\lambda \in \Lambda }\subset X}$が存在し、${\displaystyle O=\bigcup _{x_{\lambda }\in \Lambda }B_{\varepsilon _{\lambda }}(x_{\lambda })}$が成立する。

系 ― 開球は${\displaystyle {\mathcal {O}}_{d}}$の開集合である。

命題 ―  (X ,d )を距離空間とし、f : X → Xを連続な全単射で逆写像も連続なものとする。このとき、

${\displaystyle d'(x,y)=d(f(x),f(y))}$

と定義すると、dとd'はX上に同一の位相構造を定める。

定義 (ノルム) ―  Kを${\displaystyle \mathbb {R} }$もしくは${\displaystyle \mathbb {C} }$とするとき、K上ベクトル空間Vのノルムとは写像

${\displaystyle \|\cdot \|~:~V\to K}$

で以下の3性質を満たすものの事である。ここでx、yはVの元でαはKの元である：

1. ‖ x ‖ = 0 ⇔ x = 0
2. ‖ ax ‖ = |a|‖ x ‖
3. ‖ x + y ‖ ≤ ‖ x ‖ + ‖ y ‖

定義・定理 (ノルムの同値性と位相) ―  Vを（実もしくは複素）ベクトル空間とし、${\displaystyle \|\cdot \|}$と${\displaystyle \|\cdot \|'}$をV上定義された2つのノルムとする。${\displaystyle \|\cdot \|}$、${\displaystyle \|\cdot \|'}$が

${\displaystyle \exists C_{1},C_{2}>0\forall x\in V~:~C_{1}\|x\|'\leq \|x\|\leq C_{2}\|x\|'}$

を満たすとき、${\displaystyle \|\cdot \|}$、${\displaystyle \|\cdot \|'}$は同値なノルムであるという。

${\displaystyle \|\cdot \|}$、${\displaystyle \|\cdot \|'}$が同値であれば、これらのノルムが定める距離

${\displaystyle d(x,y)=\|x-y\|}$、${\displaystyle d'(x,y)=\|x-y\|'}$

は V上に同一の位相を定める。

命題 ―  有限次元の（実もしくは複素）ベクトル空間上定義されるノルムは全て同値である。

定義・定理 ― Xを集合とする。このとき以下は位相の公理を満たす。

• 空集合${\displaystyle \emptyset }$と全体集合Xのみを開集合とする位相を密着位相という。
• Xの任意の部分集合を開集合とする位相をXの離散位相という。
• Xの任意の有限部分集合と全体集合を閉集合とする位相をXの補有限位相という。
• Xの任意の可算部分集合と全体集合を閉集合とする位相をXの補可算位相（英語版）という。

定義 (内点、外点、境界点^[2]) ―  ${\displaystyle (X,{\mathcal {O}})}$を位相空間とし、AをX の部分集合とする。このとき、

• x ∈ X がAの内点であるとは、ある開集合O ⊂ Xが存在し、x ∈ O ⊂ Aが成立する事をいう。
• A^cの内点をAの外点と呼ぶ。
• Aの内点でも外点でもない 点x ∈ XをAの境界点という。

定義 (内部、外部、境界^[2]) ―  ${\displaystyle (X,{\mathcal {O}})}$を位相空間とし、AをX の部分集合とする。このとき、

• Aの内点全体の集合をAの内部（ないぶ, 英: interior）または開核といい、${\displaystyle A^{\circ },\operatorname {Int} A}$などと表す。
• Aの外点全体の集合をの外部（がいぶ, 英: exterior）といい、${\displaystyle A^{e},\ \ \operatorname {Ext} A}$などと表す。
• 境界点全体の集合をAの境界（きょうかい, 英: frontier）とい、${\displaystyle \operatorname {Fr} A,\ \operatorname {Bd} A,\ \partial A}$ などと表す。

定理・定義 (閉包、触点) ―  ${\displaystyle (X,{\mathcal {O}})}$を位相空間とし、A をX の部分集合とする。このとき、

• ${\displaystyle A^{\circ }\cup \operatorname {Fr} (A)}$をA の閉包（へいほう, 英: closure）と呼び、${\displaystyle {\bar {A}},~\operatorname {Cl} (A),~A^{-}}$などと表す。
• Aの閉包の元をAの触点という。

命題 (内部と閉包の関係) ― 　

• ${\displaystyle {\overline {A^{c}}}=(A^{\circ })^{c}}$

命題 ― 　

• x ∈ XがAの外点 ⇔ x ∈ Oを満たすある開集合O ⊂ Xが存在し、O ⊂ A^c
• x ∈ XがAの境界点 ⇔ x ∈ Oを満たす任意の開集合O ⊂ Xに対し、${\displaystyle A\cup O\neq \emptyset }$ かつ ${\displaystyle A^{c}\cup O\neq \emptyset }$
• x ∈ XがAの触点 ⇔ x ∈ Oを満たす任意の開集合O ⊂ Xに対し、${\displaystyle A\cap O\neq \emptyset }$

命題 ― 　 位相空間${\displaystyle (X,{\mathcal {O}})}$の任意の部分集合Aに対し次が成立する：

• 内部、境界、外部は、全空間X を排他的に分割する。すなわち、${\displaystyle A^{\circ }\sqcup \operatorname {Fr} (A)\sqcup A^{e}=X}$
• ${\displaystyle A^{\circ }\subset A\subset {\bar {A}}}$
• Aの内部、外部は開集合で、境界、閉包は閉集合である。

命題 (内部および閉包の特徴づけ) ― 　 位相空間${\displaystyle (X,{\mathcal {O}})}$の任意の部分集合Aに対し次が成立する：

• ${\displaystyle A^{\circ }}$はAに含まれる最大の開集合${\displaystyle \bigcup _{O\in {\mathcal {O}},O\subset A}O}$に一致する^[2]。
• ${\displaystyle {\bar {A}}}$はAを含む最小の閉集合${\displaystyle \bigcap _{F\in {\mathcal {F}},A\subset F}F}$に一致する^[2]。

定理 (内部の性質) ―  位相空間Xの任意の部分集合A、Bに対し、以下が成立する^[2]：

1. ${\displaystyle A^{\circ }\subset A}$
2. ${\displaystyle (A^{\circ })^{\circ }=A^{\circ }}$
3. ${\displaystyle (A\cap B)^{\circ }=A^{\circ }\cap B^{\circ }}$
4. ${\displaystyle X^{\circ }=X}$

定理 (クラトウスキイの公理系^[3][4]) ―  位相空間Xの任意の部分集合A、Bに対し、以下が成立する：

1. ${\displaystyle A\subset {\overline {A}}}$
2. ${\displaystyle {\overline {\overline {A}}}={\overline {A}}}$
3. ${\displaystyle {\overline {A\cup B}}={\overline {A}}\cup {\overline {B}}}$
4. ${\displaystyle {\overline {\emptyset }}=\emptyset }$

定理 (内核作用素による位相の特徴づけ^[2]) ―  Xを集合とし、Xの冪集合からそれ自身への写像

${\displaystyle \mathrm {Int} ~:~{\mathfrak {P}}(X)\to {\mathfrak {P}}(X)}$

で、${\displaystyle A^{\circ }:=\mathrm {Int} (A)}$が「定理（内核作用素の性質）」で述べた4性質を満たすものとする。

このときX上の位相構造${\displaystyle {\mathcal {O}}}$で位相空間${\displaystyle (X,{\mathcal {O}})}$の内核作用素が${\displaystyle \mathrm {Int} }$に一致するものがただ一つ存在する ${\displaystyle {\mathcal {O}}}$の開集合系${\displaystyle {\mathcal {O}}}$は具体的には以下のように書ける：

${\displaystyle {\mathcal {O}}=\{O\subset X\mid O=\mathrm {Int} (O)\}}$

定理 (閉包作用素による位相の特徴づけ) ―  Xを集合とし、Xの冪集合からそれ自身への写像

${\displaystyle \mathrm {Cl} ~:~{\mathfrak {P}}(X)\to {\mathfrak {P}}(X)}$

で、${\displaystyle {\bar {A}}:=\mathrm {Cl} (A)}$がクラトウスキイの公理系を満たすものとする。

このときX上の位相構造${\displaystyle {\mathcal {O}}}$で位相空間${\displaystyle (X,{\mathcal {O}})}$の閉包作用素が${\displaystyle {\bar {A}}=\mathrm {Cl} (A)}$に一致するものがただ一つ存在する^[3][4]。 ${\displaystyle {\mathcal {O}}}$の閉集合系${\displaystyle {\mathcal {F}}}$は具体的には以下のように書ける：

${\displaystyle {\mathcal {F}}=\{F\subset X\mid F={\bar {F}}\}}$

定義 (集積点、導集合、孤立点) ―  ${\displaystyle (X,{\mathcal {O}})}$を位相空間とし、AをXの部分集合とする。このとき、

• x∈Xが${\displaystyle A\setminus \{x\}}$の触点であるとき、xをAの集積点という^[2]。
• Aの集積点全体の集合を導集合といい、A^dと表す^[2]。
• ${\displaystyle A\setminus A^{d}}$の元をAの孤立点という^[2]。

命題 ― 　

• x ∈ XがAの集積点 ⇔ x ∈ Oを満たす任意の開集合O ⊂ Xに対し、Oはx以外にAの元を含む。
• x ∈ XがAの孤立点 ⇔ x ∈ Aであり、しかもx ∈ Oを満たすある開集合O ⊂ Xがあって、Oはx以外にAの元を含まない。

定義 (稠密) ―  Aが位相空間${\displaystyle (X,{\mathcal {O}})}$の稠密な部分集合であるとは、A の閉包が X に一致することである。

定義 (近傍系、開近傍系) ―  ${\displaystyle (X,{\mathcal {O}})}$を位相空間とし、xをXの点とする。このとき、

x ∈ O

を満たす開集合をxの開近傍（かいきんぼう, 英: open neighborhood）という。 またX の部分集合Nが以下を満たすとき、Nはxの 近傍（きんぼう, 英: neighborhood）であるという^[5]

ある開集合O ⊂ Xが存在し、x ∈ O ⊂ N

点xの近傍全体の集合をxの近傍系といい^[5]、xの開近傍全体の集合をxの開近傍系という。

定義 (基本近傍系) ―  ${\displaystyle (X,{\mathcal {O}})}$を位相空間とし、xをXの点とし、${\displaystyle {\mathcal {N}}_{x}}$をxの近傍系とする。${\displaystyle {\mathcal {N}}_{x}}$の部分集合${\displaystyle {\mathcal {B}}_{x}}$が以下を満たすとき、${\displaystyle {\mathcal {B}}_{x}}$をxにおける基本近傍系という^[6]：

任意の近傍${\displaystyle N\in {\mathcal {N}}_{x}}$に対し、ある${\displaystyle B\in {\mathcal {B}}_{x}}$が存在し、x ∈ B ⊂ N

命題 ― 　 ${\displaystyle {\mathcal {B}}_{x}}$を位相空間${\displaystyle (X,{\mathcal {O}})}$の点xにおける基本近傍系とする。このとき、

• x ∈ XがAの内点 ⇔ ${\displaystyle \exists N\in {\mathcal {B}}_{x}~:~N\subset A}$
• x ∈ XがAの外点 ⇔ ${\displaystyle \exists N\in {\mathcal {B}}_{x}~:~N\subset A^{c}}$
• x ∈ XがAの境界点 ⇔ ${\displaystyle \forall N\in {\mathcal {B}}_{x}~:~A\cup N\neq \emptyset }$ かつ ${\displaystyle A^{c}\cup N\neq \emptyset }$
• x ∈ XがAの触点 ⇔ ${\displaystyle \forall N\in {\mathcal {B}}_{x}~:~A\cap N\neq \emptyset }$
• x ∈ XがAの集積点 ⇔ ${\displaystyle \forall N\in {\mathcal {B}}_{x}~:~}$Nはx以外にAの元を含む。

定義 (ハウスドルフの公理系^[5]) ―  点xの近傍系を${\displaystyle {\mathcal {N}}_{x}}$で表すとき、Xの任意の部分集合N、N'、Mに対して以下が成立する。

• ${\displaystyle N,N'\in {\mathcal {N}}_{x}\Rightarrow N\cap N'\in {\mathcal {N}}_{x}}$
• ${\displaystyle N\in {\mathcal {N}}_{x},~M\supset N\Rightarrow M\in {\mathcal {N}}_{x}}$
• ${\displaystyle N\in {\mathcal {N}}_{x}}$であれば、ある${\displaystyle L\in {\mathcal {N}}_{x}}$が存在し全ての${\displaystyle y\in L}$に対して${\displaystyle N\in {\mathcal {N}}_{y}}$

定理 (近傍系による位相の特徴づけ) ―  Xを集合とし、Xの元にXの冪集合の冪集合の元を対応させる写像

${\displaystyle {\mathcal {N}}\colon X\to {\mathfrak {P}}({\mathfrak {P}}(X)),~x\mapsto {\mathcal {N}}_{x}}$

がハウスドルフの公理系を満たしたとする。このときX上の位相構造${\displaystyle {\mathcal {O}}}$で位相空間${\displaystyle (X,{\mathcal {O}})}$の各点xの近傍が${\displaystyle {\mathcal {N}}_{x}}$に一致するものがただ一つ存在する^[5]。 ${\displaystyle {\mathcal {O}}}$は具体的には以下のように書ける：

${\displaystyle {\mathcal {O}}=\{O\subset X\mid \forall x\in O~:~O\in {\mathcal {N}}_{x}\}}$

定義 (距離空間における点列の収束) ―  ${\displaystyle (X,d)}$を距離空間とする。Xの点列${\displaystyle (x_{n})_{n\in \mathbb {N} }}$がXの点xに収束するとは以下が成立する事を言う：

${\displaystyle \forall \varepsilon >0\exists n_{0}\in \mathbb {N} \forall n>n_{0}~:~x_{n}\in B_{\varepsilon }(x)}$

ここで、${\displaystyle B_{\varepsilon }(x)=\{y\in X|d(y,x)<\varepsilon \}}$である。

定義 (有向集合) ―  空でない集合ΛとΛ上の二項関係「≤ 」の組 (Λ, ≤)が有向集合（ゆうこうしゅうごう、英: directed set）であるとは、「≤ 」が以下の性質を全て満たす事を言う^[7]:

• （反射律）∀λ∈Λ : λ ≤λ
• （推移律）∀λ,μ,ν∈Λ : λ ≤ μ, μ ≤ν ⇒ λ ≤ ν
• Λの任意の二元が上界を持つ。すなわち∀λ,μ∈Λ∃ν∈Λ : λ ≤ ν, μ ≤ν

定義 (有向点族) ― 集合X上の有向点族とは、X上の族(x_λ)_λ∈Λで添字集合Λが有向集合であるものを指す^{[7][注 5]}。有向点族はネット (英: net)、 Moore-Smith 列(英: Moore-Smith sequence^[8])、generalized sequence^[8]などとも呼ばれる。

命題 (開近傍系を添字集合に取る有向点族) ―  aを位相空間Xの点とし、${\displaystyle {\mathcal {V}}_{a}}$をaの開近傍系とする。このとき${\displaystyle {\mathcal {V}}_{a}}$上の二項関係

${\displaystyle U\leq V~:\!\iff V\supset U~~~~{\text{for }}U,V\in {\mathcal {V}}_{a}}$

を入れると、${\displaystyle ({\mathcal {V}}_{a},\leq )}$は有向集合である。よって${\displaystyle {\mathcal {V}}_{a}}$を添え字に取るX上の任意の族${\displaystyle (x_{U})_{U\in {\mathcal {V}}_{a}}}$はこの二項関係に関して有向点族である。

定義 (部分有向点族) ―  Xを集合とし、X上の有向点族${\displaystyle (y_{\gamma })_{\gamma \in \Gamma }}$、${\displaystyle (x_{\lambda })_{\lambda \in \Lambda }}$に対し、以下の性質を満たすh : Γ→Λが存在するとき、${\displaystyle (y_{\gamma })_{\gamma \in \Gamma }}$は${\displaystyle (x_{\lambda })_{\lambda \in \Lambda }}$の部分有向点族という^[9]：

1. ${\displaystyle \forall \gamma \in \Gamma ~:~y_{\gamma }=x_{h(\gamma )}}$
2. ${\displaystyle \forall \lambda \in \Lambda \exists \gamma _{0}\in \Gamma \forall \gamma \in \Gamma ~:~\gamma \geq \gamma _{0}\Rightarrow h(\gamma )\geq \lambda }$

（2を強共終性(英: strong cofinality^[10])という）

定義 (有向点族の収束) ―  ${\displaystyle (X,{\mathcal {O}})}$を位相空間とする。X上の有向点族${\displaystyle x=(x_{\lambda })_{\lambda \in \Lambda }}$がa∈Xに収束するとは、

∀U (a の近傍) ${\displaystyle \exists \lambda _{0}\in \Lambda \forall \lambda >\lambda _{0}~~:~~x_{\lambda }\in U}$

が成立する事をいう^[7]。${\displaystyle x=(x_{\lambda })_{\lambda \in \Lambda }}$の収束先aが一意であれば、

${\displaystyle \lim _{\lambda \to \infty }x_{\lambda }=a}$、${\displaystyle \lim _{\Lambda }x=a}$

等と表す。

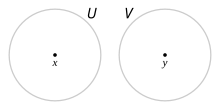
定理・定義 (ハウスドルフ性) ―  位相空間${\displaystyle (X,{\mathcal {O}})}$において、下記の２つの性質は同値である。これらの性質の１つ（したがって両方を満たす事）をハウスドルフ性もしくはハウスドルフの分離公理といい、ハウスドルフ性が成り立つ位相空間をハウスドルフ空間もしくはT₂-空間という^[12]。

• X上の任意の有向点族${\displaystyle (x_{\lambda })_{\lambda \in \Lambda }}$に対し、 ${\displaystyle (x_{\lambda })_{\lambda \in \Lambda }}$が収束すればその収束先は一意である。
• X上の任意の2点x、yに対し、xの開近傍Uと、yの開近傍Vが存在しU∩V'=∅

定理 (有向点族による特徴づけ) ―  Aを位相空間Xの任意の部分集合とき、以下が成立する：

• Aは閉集合である⇔A上の有向点族(x_λ)_λ∈Λでa∈Xに収束するものがあれば、a∈Aである^[13]。
• 点aがAの閉包に含まれる⇔A上のある有向点族(x_λ)_λ∈Λが存在し、(x_λ)_λ∈Λはaに収束する^[13]。
• 点aがAの集積点である⇔${\displaystyle A\setminus \{a\}}$上のある有向点族(x_λ)_λ∈Λが存在し、(x_λ)_λ∈Λはaに収束する^[13]。

命題・定義 (有向集合の直積) ―  (Γ_λ)_λ∈Γを有向集合の族とするとき、(Γ_λ)_λ∈Γの集合としての直積 ${\displaystyle {\underset {\lambda \in \Lambda }{\times }}\Gamma _{\lambda }}$に

${\displaystyle (\gamma _{\lambda })_{\lambda \in \Lambda }\geq (\xi _{\lambda })_{\lambda \in \Lambda }~:\iff \forall \lambda \in \Lambda ~:~\gamma _{\lambda }\geq \xi _{\lambda }}$

という順序を入れると、${\displaystyle {\underset {\lambda \in \Lambda }{\times }}\Gamma _{\lambda }}$は有向集合になる。この順序をいれた${\displaystyle {\underset {\lambda \in \Lambda }{\times }}\Gamma _{\lambda }}$を (Γ_λ)_λ∈Γの有向集合としての直積という。

定理 (二重極限の定理（英: Theorem on Iterated limit^[14]）) ―  Λを有向集合とし、各λ∈Λに対し、Γ_λを有向集合とし、${\displaystyle (X,{\mathcal {O}})}$を位相空間とする。 各λ∈Λに対し、有向集合Γ_λを添え字とするX上の有向点族${\displaystyle x_{\lambda }=(x_{\lambda ,\gamma })_{\gamma \in \Gamma _{\lambda }}}$が、y_λに収束するとし、さらに有向点族${\displaystyle (y_{\lambda })_{\lambda \in \Lambda }}$がzに収束するものとする。

(Γ_λ)_λ∈Λの直積を${\displaystyle \Gamma ={\underset {\lambda \in \Lambda }{\times }}\Gamma _{\lambda }}$とし、有向点族${\displaystyle (w_{\lambda ,\xi })_{(\lambda ,\xi )\in \Lambda \times \Gamma }=(x_{\lambda ,\xi _{\lambda }})_{(\lambda ,\xi )\in \Lambda \times \Gamma }}$を考える（ただし${\displaystyle \xi =(\xi _{\lambda })_{\lambda \in \Lambda }\in \Gamma ={\underset {\lambda \in \Lambda }{\times }}\Gamma _{\lambda }}$と定める）。

このとき${\displaystyle (w_{\lambda ,\xi })_{(\lambda ,\xi )\in \Lambda \times \Gamma }}$はzに収束する^[14][15]。

定理 (極限による位相の特徴づけ^[16][15]) ―  Xを集合とし、${\displaystyle {\mathcal {C}}}$をX上の有向点族とXの点の組からなるクラスとする。

${\displaystyle ((x_{\lambda })_{\lambda \in \Lambda },y)\in {\mathcal {C}}}$であるとき${\displaystyle (x_{\lambda })_{\lambda \in \Lambda }}$がyに${\displaystyle {\mathcal {C}}}$-収束するという事にするとき、以下が成立するとする：

• x_λが恒等的にyに等しければ、${\displaystyle (x_{\lambda })_{\lambda \in \Lambda }}$はyに${\displaystyle {\mathcal {C}}}$-収束する
• ${\displaystyle (x_{\lambda })_{\lambda \in \Lambda }}$がyに${\displaystyle {\mathcal {C}}}$-収束するとき、${\displaystyle (x_{\lambda })_{\lambda \in \Lambda }}$の任意の部分有向点族もyに${\displaystyle {\mathcal {C}}}$-収束する
• ${\displaystyle (x_{\lambda })_{\lambda \in \Lambda }}$がyに${\displaystyle {\mathcal {C}}}$-収束しないとき、${\displaystyle (x_{\lambda })_{\lambda \in \Lambda }}$の部分有向点族${\displaystyle (x_{\lambda _{\gamma }})_{\gamma \in \Gamma }}$で${\displaystyle (x_{\lambda _{\gamma }})_{\gamma \in \Gamma }}$のいかなる部分有向点族もyに${\displaystyle {\mathcal {C}}}$-収束しないものが存在する。
• 二重極限の定理で「収束」を「${\displaystyle {\mathcal {C}}}$-収束」に置き換えたものを満たす。

このときX上の位相構造${\displaystyle {\mathcal {O}}}$で${\displaystyle (X,{\mathcal {O}})}$における有向点族の収束が${\displaystyle {\mathcal {C}}}$-収束に一致するものが唯一存在する。${\displaystyle {\mathcal {O}}}$における閉包作用素は具体的には以下のように書ける：

${\displaystyle {\bar {A}}={\Bigg \{}y\in X~{\Bigg |}~\exists (x_{\lambda })_{\lambda \in \Lambda }\subset A~:~(x_{\lambda })_{\lambda \in \Lambda }}$はyに${\displaystyle {\mathcal {C}}}$-収束する${\displaystyle {\Bigg \}}}$

定義・定理 (一点における連続性) ―  ${\displaystyle (X,{\mathcal {O}}_{X})}$、${\displaystyle (Y,{\mathcal {O}}_{Y})}$を位相空間とし、f: X → Yを写像とし、xをXの点とする。このとき以下の２条件は同値であり、この２条件の一方（したがって両方）を満たすとき、fはx∈Xで連続(英: continuous)であるという。以下で${\displaystyle {\mathcal {N}}_{x}}$はxの(開とは限らない)近傍全体を表す：

• xに収束する任意の有向点族${\displaystyle (x_{\lambda })_{\lambda \in \Lambda }}$に対し、${\displaystyle (f(x_{\lambda }))_{\lambda \in \Lambda }}$は${\displaystyle f(x)}$に収束する。
• f(x)の近傍のfによる逆像はxの近傍である。すなわち、
  　　${\displaystyle \forall N\in {\mathcal {N}}_{f(x)}~:~f^{-1}(N)\in {\mathcal {N}}_{x}}$

定理 (連続性の特徴づけ) ―  ${\displaystyle f~:~(X,{\mathcal {O}}_{X})\to (Y,{\mathcal {O}}_{Y})}$を位相空間から位相空間への関数とするとき、以下は同値である。

• fは連続である。
• 開集合の逆像は開集合である。すなわち${\displaystyle \forall O\in {\mathcal {O}}_{Y}~:~f^{-1}(O)\in {\mathcal {O}}_{X}}$である^[17]。
• 閉集合の逆像は閉集合である。すなわち${\displaystyle \forall F\in {\mathcal {F}}_{Y}~:~f^{-1}(F)\in {\mathcal {F}}_{X}}$である^[17]。
• 任意のA⊂Xに対し${\displaystyle f({\bar {A}})\subset {\overline {f(A)}}}$^[17]。

定義 (位相同型) ―  ${\displaystyle (X,{\mathcal {O}}_{X})}$、${\displaystyle (Y,{\mathcal {O}}_{Y})}$を位相空間とし、f : X → Y を写像とするとき、f が同相写像であるとは、f が全単射で、しかもf と f⁻¹ が両方とも連続であることをいう。

また、X、Y 間に同相写像が存在するとき、${\displaystyle (X,{\mathcal {O}}_{X})}$、${\displaystyle (Y,{\mathcal {O}}_{Y})}$は位相同型もしくは同相であるという。