空格子近似

空格子近似はポテンシャルが周期的で弱い (一定に近い) 理論的な電子バンド構造のモデルである。ポテンシャルが周期的ではない空[要説明]格子不規則格子を考えうる[1]。空格子近似は結晶格子中を移動する非相互関係の自由電子のエネルギー分散関係の多くの特性を記述することができる。「空格子」中の電子のエネルギーは自由電子のエネルギーと同じである。このモデルは有用である。なぜなら全ての電子バンド構造にとって基本的な固体におけるエネルギー分散関係の、時に示す非常に複雑な特徴に明確な説明を与えるからである。

散乱と周期性

1次元格子における自由電子のバンド

この自由電子のモデルにおける格子の周期ポテンシャルは弱くなくてはならない。そうでなくては電子は自由ではなくなるからである。散乱の強さは主に系の形状およびトポロジーに依存している。散乱断面積のようにトポロジカル的に定義されたパラメータは、ポテンシャルの大きさとポテンシャル井戸の大きさに依存している。1次元、2次元、3次元の空間では、ポテンシャル井戸はポテンシャルの大きさや符号や大きさがどれくらい制限されるかに関わらず常に波を散乱させる。一次元格子の粒子の場合、クローニッヒ・ペニーモデルのようにポテンシャル、格子間隔、ポテンシャル井戸の大きさの値を代入することにより、分析的にバンド構造を計算することができる[2]。2次元及び3次元の問題では、いくつかのパラメータを有する類似のモデルに基づいて正確にバンド構造を計算するのはより難しいことである。それでもなお、バンド構造の特性は摂動法を用いることでほとんどの領域で容易に近似をすることができる。

理論的には、格子は無限大の大きさなので、弱い周期的散乱ポテンシャルは最終的に波を反射するのに十分な強さになる。散乱の過程は結晶構造の周期的ポテンシャルによる良く知られた電子のブラッグ反射をもたらす。これは分散関係とブリルアンゾーンにおけるk空間の分割の周期性の原因である。周期的エネルギー分散関係は以下の式で表される。

E n ( k ) = ℏ 2 ( k + G n ) 2 2 m {\displaystyle E_{n}(\mathbf {k} )={\frac {\hbar ^{2}(\mathbf {k} +\mathbf {G} _{n})^{2}}{2m}}}

G n {\displaystyle \mathbf {G} _{n}} は E n ( k ) {\displaystyle E_{n}(\mathbf {k} )} のバンドの逆格子ベクトル[要説明]である。

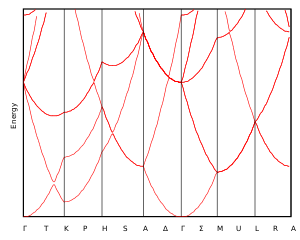
右図は、長さaの格子単位を持つ1次元格子の逆空間における3つの周期の分散関係を示している。

エネルギーバンド及び状態密度

1次元格子では、エネルギー間のバンドを決定する逆格子ベクトル  G n {\displaystyle \mathbf {G} _{n}}  の数はエネルギーが上がると2に限られる。2次元及び3次元格子においては自由電子バンド  E n ( k ) {\displaystyle E_{n}(\mathbf {k} )}  を決定する逆格子ベクトルの数は波数ベクトルの長さやエネルギーが大きくなると、急速に増加する。これは区間  [ k , k + d k ] {\displaystyle [\mathbf {k} ,\mathbf {k} +d\mathbf {k} ]}  にある逆格子ベクトル G n {\displaystyle \mathbf {G} _{n}} の数が増えるからである。エネルギー間  [ E , E + d E ] {\displaystyle [E,E+dE]}  における状態密度は、逆格子空間での  [ k , k + d k ] {\displaystyle [\mathbf {k} ,\mathbf {k} +d\mathbf {k} ]}  における状態数と分散関係  E n ( k ) {\displaystyle E_{n}(\mathbf {k} )} の勾配による。

図3:3次元k空間における自由電子の状態密度

格子セルは球対称ではないが、分散関係が中心のブリルアンゾーンより外側に広がると、逆格子セル内の中心の定点から見ると球の対称性を持つ。3次元格子の状態密度は格子がない場合と同じである。3次元の場合、状態密度  D 3 ( E ) {\displaystyle D_{3}\left(E\right)}  は

D 3 ( E ) = 2 π E − E 0 c k 3   . {\displaystyle D_{3}\left(E\right)=2\pi {\sqrt {\frac {E-E_{0}}{c_{k}^{3}}}}\ .}

となる。3次元空間においてブリルアンゾーンの境界は平面である。分散関係は、全ての可能な逆格子ベクトルに対する自由電子のエネルギー分散の放物線による円錐曲線を示す。これにより、分散関係が計算される際に1次と高次ブリルアンゾーン境界、分散放物線の交差円錐、評価曲線の間に可能な角度が多数あるため、曲線の非常に複雑な交差の組み合わせになる。

第2、第3及びそれ以上のブリルアンゾーン

面心立方格子のブリルアンゾーン

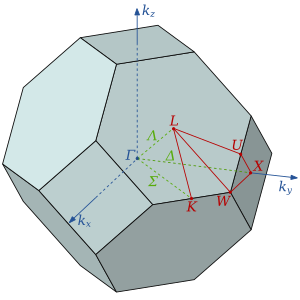
第1ブリルアンゾーンより外側を波動ベクトル  k {\displaystyle \mathbf {k} }  を持つ固体の格子を通って移動する「自由電子」は、第1ブリルアンゾーンに跳ね返る。その例と図は外部リンクを参照せよ。

ほとんど自由な電子のモデル

アルミニウムのようなほとんどの単純金属では、スクリーニング効果により固体中のイオンの電界が大きく減少する。静電ポテンシャルは以下の式で表される。

V ( r ) = Z e r e − q r {\displaystyle V(r)={\frac {Ze}{r}}e^{-qr}}

Z は原子番号、e は電荷の基本単位、r は埋め込まれたイオンである核への距離、q はポテンシャルの範囲を決定するスクリーニングのパラメータである。格子ポテンシャル  V ( r ) {\displaystyle V(\mathbf {r} )} のフーリエ変換 U G {\displaystyle U_{\mathbf {G} }} は、ハミルトニアンの逆格子ベクトル間の非対角要素  U G {\displaystyle U_{\mathbf {G} }}  の値がほとんど0になるとき以下の式で表される。

U G = 4 π Z e q 2 + G 2 {\displaystyle U_{\mathbf {G} }={\frac {4\pi Ze}{q^{2}+\mathbf {G} ^{2}}}}

その結果、バンドギャップの大きさ  2 | U G | {\displaystyle 2|U_{\mathbf {G} }|}  が崩れ、空格子近似が得られる。

一般的な金属結晶の電子バンド

いくつかのエキゾチックな場合の例外を除き、金属は3種類の結晶構造を持つ。体心立方格子 (BCC)、面心立方格子 (FCC) の立方晶系、六方最密充填構造 (HCP)の3種類である。

  • 体心立方格子 (I)
    体心立方格子 (I)
  • 面心立方格子 (F)
    面心立方格子 (F)
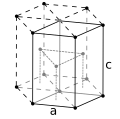  • 六方最密構造
    六方最密構造
BCCでの自由電子のバンド
FCCでの自由電子のバンド
HCPでの自由電子のバンド

脚注

[脚注の使い方]
  1. ^ Physics Lecture Notes. P.Dirac, Feynman,R.,1968. Internet, Amazon,25.03.2014.
  2. ^ C. Kittel (1953–1976). Introduction to Solid State Physics. Wiley & Sons. ISBN 0-471-49024-5 

外部リンク

  • Brillouin Zone simple lattice diagrams by Thayer Watkins
  • Brillouin Zone 3d lattice diagrams by Technion.
  • DoITPoMS Teaching and Learning Package- "Brillouin Zones"