Conjunto de Julia

No contexto de dinâmica complexa, um tópico da matemática, o conjunto de Julia e o conjunto de Fatou são dois conjuntos complementares definidos por uma função. Informalmente, o conjunto de Fatou de uma função consiste nos valores com a propriedade de que todos os valores próximos comportam-se de forma similar por iterações repetidas, e o conjunto de Julia consiste dos valores tais que uma perturbação arbitrariamente pequena pode causar mudanças drásticas na sequência de valores iterados da função. Assim, o comportamento da função do conjunto de Fatou é dito 'regular', enquanto no conjunto de Julia ele é 'caótico'.

O conjunto de Julia de uma função ${\displaystyle f}$ é usualmente denotado ${\displaystyle J(f)}$, e o conjunto de Fatou denotado ${\displaystyle F(f)}$.^[1] Esses conjuntos tem seu nome em homenagem aos matemáticos franceses Gaston Julia^[2] e Pierre Fatou,^[3] cujos trabalhos começaram o estudo de dinâmica complexa no início do século XX.

Polinômios quadráticos

Um exemplo de sistema dinâmico complexo é o da família de polinômios quadráticos, um caso especial de mapa racional. O polinômio quadrático pode ser expresso como:

${\displaystyle f_{c}(z)=z^{2}+c\,}$

(onde o parâmetro ${\displaystyle c\,}$ é um número complexo)

• 
  Filled Conjunto de Julia para f_c, c=1−φ onde φ é a razão áurea
• 
  Conjunto de Julia para f_c, c=(φ−2)+(φ−1)i =-0.4+0.6i
• 
  Conjunto de Julia para f_c, c=0.285+0i
• 
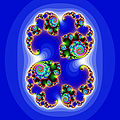  Conjunto de Julia para f_c, c=0.285+0.01i
• 
  Conjunto de Julia para f_c, c=0.45+0.1428i
• 
  Conjunto de Julia para f_c, c=-0.70176-0.3842i
• 
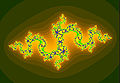  Conjunto de Julia para f_c, c=-0.835-0.2321i

Nesse caso, os valores do parâmetro ${\displaystyle c}$ para os quais o conjunto de Julia é conexo formam o conjunto de Mandelbrot.

Quaterniões

• 
  Conjunto de Julia gerado por uma função dos quaterniões.
• Fatias tridimensionais através do conjunto de Julia (quadri-dimensional) de uma função dos quaterniões.

Conjunto de Julia Cheio

Seja ${\displaystyle P:\mathbb {C} \cup \{\infty \}\rightarrow \mathbb {C} \cup \{\infty \}}$ um polinômio complexo mônico de grau ${\displaystyle d\geq 2}$. Denotamos por ${\displaystyle P^{n}}$ a ${\displaystyle n-}$ésima iterada de ${\displaystyle P}$. O Conjunto de Julia Cheio de ${\displaystyle P}$ é definido por

${\displaystyle K(P)=\{z:P^{n}(z),{\text{nâo tende para }}\infty \}}$

Com a definição de conjunto de Julia Cheio e com a definição do conjunto de Julia, observamos que o conjunto de Julia é o bordo do conjunto de Julia Cheio:

${\displaystyle J(f)=\partial K(f)}$

Exemplos

• 
  Conjunto de Julia Cheio P(z) =z²−0.4+0.6i.
• 
  Conjunto de Julia Cheio P(z) =z² −0.8 + 0.156i.
• 
  Conjunto de Julia Cheio P(z) =z²+ 0.285 + 0.01i.
• 
  Conjunto de Julia Cheio P(z) =z² -1.476.

Ver também

O Commons possui imagens e outros ficheiros sobre Conjunto de Julia

• Conjunto limite
• Conjuntos estáveis e instáveis
• Teoria do caos

Referências