Операция «Snub»
 Плосконосый куб или плосконосый кубооктаэдр |  Плосконосый додекаэдр или плосконосый икосододекаэдр |


Операция snub или отсечение вершин — это операция, применяемая к многогранникам. Термин появился из названий, данных Кеплером двум архимедовым телам — плосконосый куб (cubus simus) и плосконосый додекаэдр (dodecaedron simum)[1]. В общем случае плосконосые формы имеют хиральную симметрию двух видов, с ориентацией по часовой стрелке и против часовой стрелки. Согласно названиям Кеплера, отсечение вершин можно рассматривать как растяжение правильного многогранника, когда исходные грани отодвигаются от центра и поворачиваются относительно центров, вместо исходных вершин добавляются многоугольники с центрами в этих вершинах, а пары треугольников заполняют пространство между исходными рёбрами.
Терминологию обобщил Коксетер со слегка другим определением для более широкого множества однородных многогранников.
Операция «snub» Конвея
Джон Конвей исследовал обобщённые операции над многогранниками, определяя то, что называется теперь нотацией Конвея для многогранников, которая может быть применена к многогранникам и мозаикам. Конвей назвал операцию Коксетера semi-snub (полу-snub)[2].
В этой нотации snub определяется как композиция двойственного и gyro операторов, , и это эквивалентно последовательности операторов альтернирования[англ.], усечения и ambo. Нотация Конвея избегает операции альтернирования, поскольку та применима только к многогранниками с гранями, имеющими чётное число сторон.
| Многогранники | Евклидовы мозаики | Гиперболические мозаики | ||||
|---|---|---|---|---|---|---|
| Нотация Конвея | sT | sC = sO | sI = sD | sQ | sH = sΔ | sΔ7 |
| Плосконосый многогранник | Тетраэдр | Куб или Октаэдр | Икосаэдр или Додекаэдр | Квадратная мозаика | Шестиугольная мозаика или Треугольная мозаика | Семиугольная мозаика или Треугольная мозаика порядка 7[англ.] |
  |   |   |   |   |   | |
| Рисунок |  |  |  |  |  |  |
В 4-мерных пространствах Конвей считает, что плосконосый 24-ячейник[англ.] должен называться полуплосконосым 24-ячейником, поскольку он не представляет альтернированный всеусечённый 24-ячейник[англ.], как его аналог в 3-мерном пространстве. Вместо этого он является альтернированным усечённым 24-ячейником[англ.][3].
Операции «snub» Коксетера, правильная и квазиправильная
| Исходное тело | Полноусечённый многогранник r | Усечённый многогранник t | Альтернированный многогранник[англ.] h |
|---|---|---|---|
| Cube | Кубооктаэдр Полноусечённый куб | Усечённый кубооктаэдр Скошено-усечённый куб | Плосконосый кубооктаэдр Плосконосый полноусечённый куб |
| C | CO rC | tCO trC или trO | htCO = sCO htrC = srC |
| {4,3} | или r{4,3} | или tr{4,3} | htr{4,3} = sr{4,3} |
     |    или или      |    или или      |    или или      |
 |  |  |  |
Терминология «snub» (отсечения вершин) Коксетера несколько отличается и означает альтернированное[англ.] усечение, по которому плосконосый куб получается операцией snub (отсечение вершин) из кубооктаэдра, а плосконосый додекаэдр — из икосододекаэдра. Это определение используется в названиях двух тел Джонсона — плосконосый двуклиноид и плосконосая квадратная антипризма, а также в названиях многогранников более высокой размерности, таких как 4-мерный плосконосый 24-ячейник[англ.], 





 или s{3,4,3}.
или s{3,4,3}.
Правильный многогранник (или мозаика) с символом Шлефли, и диаграммой Коксетера 



 имеет усечение, определённое как с диаграммой
имеет усечение, определённое как с диаграммой 



 , и плосконосую форму, определённую как альтернированное[англ.] усечение с диаграммой Коксетера
, и плосконосую форму, определённую как альтернированное[англ.] усечение с диаграммой Коксетера 



 . Это построение требует, чтобы q было чётным.
. Это построение требует, чтобы q было чётным.
Квазиправильный многогранник или r{p,q}, с диаграммой Коксетера 

 или
или 



 имеет квазиправильное усечение, определённое как или tr{p,q} (с диаграммой Коксетера
имеет квазиправильное усечение, определённое как или tr{p,q} (с диаграммой Коксетера 

 или
или 



 ) и квазиправильную плосконосую форму, определённую как альтернированное[англ.] усечение полного усечения или htr{p,q} = sr{p,q} (с диаграммой Коксетера
) и квазиправильную плосконосую форму, определённую как альтернированное[англ.] усечение полного усечения или htr{p,q} = sr{p,q} (с диаграммой Коксетера 

 или
или 



 ).
).
Например, плосконосый куб Кеплера получается из квазирегулярного кубооктаэдра с вертикальным символом Шлефли (и диаграммой Коксетера 

 ) и более точно называется плосконосый кубооктаэдр, который выражается символом Шлефли (с диаграммой Коксетера
) и более точно называется плосконосый кубооктаэдр, который выражается символом Шлефли (с диаграммой Коксетера 

 ). Плосконосый кубооктаэдр является альтернацией усечённого кубооктаэдра (
). Плосконосый кубооктаэдр является альтернацией усечённого кубооктаэдра (

 ).
).
Правильные многогранники с чётным порядком вершин также могут быть приведены к плосконосой форме как альтернированное усечение, подобно как плосконосый октаэдр (



 ) (и плосконосый тетратетаэдр ,
) (и плосконосый тетратетаэдр , 

 ) представляет псевдоикосаэдр, правильный икосаэдр с пиритоэдральной симметрией. Плосконосый октаэдр является альтернированной формой усечённого октаэдра, (
) представляет псевдоикосаэдр, правильный икосаэдр с пиритоэдральной симметрией. Плосконосый октаэдр является альтернированной формой усечённого октаэдра, (



 ), или в форме тетраэдральной симметрии: и
), или в форме тетраэдральной симметрии: и 

 .
.
| Усечённый t | Альтернированный h | |
|---|---|---|
| Октаэдр O | Усечённый октаэдр tO | Плосконосый октаэдр htO или sO |
| {3,4} | t{3,4} | ht{3,4} = s{3,4} |
     |      |      |
 |  |  |
Операция отсечения вершин (носов) Коксетера позволяет также определить n-антипризму как или на основе n-призм или , а является правильным осоэдром, вырожденным многогранником, который является допустимой мозаикой на сфере с двуугольными или луноподобными гранями.
| Рисунок |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|
| Диаграммы Коксетера |           |           |           |           |           |           |      ... ...     ... ... |           |
| Символ Шлефли | s{2,4} | s{2,6} | s{2,8} | s{2,10} | s{2,12} | s{2,14}[англ.] | s{2,16}[англ.]... | s{2,∞}[англ.] |
| sr{2,2} | sr{2,3} | sr{2,4} | sr{2,5} | sr{2,6} | sr{2,7} | sr{2,8}... ... | sr{2,∞} | |
| Нотация Конвея | A2 = T | A3 = O | A4 | A5 | A6 | A7 | A8... | A∞ |
Тот же процесс применим для плосконосых мозаик:
| Треугольная мозаика Δ | Усечённая треугольная мозаика tΔ | Плосконосая треугольная мозаика htΔ = sΔ |
|---|---|---|
| {3,6} | t{3,6} | ht{3,6} = s{3,6} |
     |      |      |
 |  |  |
Примеры
| Пространство | Сферическое | Евклидово | Гиперболическое | |||||
|---|---|---|---|---|---|---|---|---|
| Рисунок |  |  |  |  |  |  |  |  |
| Диаграмма Коксетера |      |      |      |      |      |      |      | ...     |
| Символ Шлефли | s{2,4} | s{3,4} | s{4,4} | s{5,4}[англ.] | s{6,4}[англ.] | s{7,4}[англ.] | s{8,4}[англ.] | ...s{∞,4}[англ.] |
| Пространство | Сферическая | Евклидово | Гиперболическое | |||||
|---|---|---|---|---|---|---|---|---|
| Рисунок |  |  |  |  |  |  |  |  |
| Диаграмма Коксетере |      |      |      |      |      |      |      | ...     |
| Символ Шлефли | sr{2,3} | sr{3,3} | sr{4,3} | sr{5,3} | sr{6,3} | sr{7,3}[англ.] | sr{8,3}[англ.] | ...sr{∞,3}[англ.] |
| Нотация Конвея | A3 | sT | sC или sO | sD или sI | sΗ или sΔ | |||
| Пространство | Сферическое | Евклидово | Гиперболическое | |||||
|---|---|---|---|---|---|---|---|---|
| Рисунок |  |  |  |  |  |  |  |  |
| Диаграмма Коксетера |      |      |      |      |      |      |      | ...     |
| Символ Шлефли | sr{2,4} | sr{3,4} | sr{4,4} | sr{5,4}[англ.] | sr{6,4}[англ.] | sr{7,4}[англ.] | sr{8,4}[англ.] | ...sr{∞,4}[англ.] |
| Нотация Конвея | A4 | sC или sO | sQ | |||||
Неоднородные плосконосые многогранники
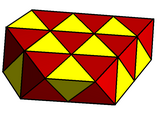
У неоднородных многогранников, для которых в вершины сходятся чётное число рёбер, могут быть отсечены вершины, включая некоторые бесконечные наборы, например:
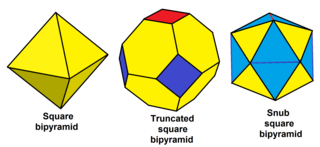 |
| Плосконосая квадратная бипирамида |
|---|
 |
| Плосконосая шестиугольная бипирамида |
 |
| Рисунок |  |  |  |  ... ... |
|---|---|---|---|---|
| Символ Шлефли | ss{2,4} | ss{2,6} | ss{2,8} | ss{2,10}... |
| ssr{2,2} | ssr{2,3} | ssr{2,4} | ssr{2,5}... |
Однородные плосконосые звёздчатые многогранники Коксетера
Плосконосые звёздчатые многогранники строятся по треугольнику Шварца (p q r) с рациональными зеркалами, в котором все зеркала активны и альтернированы.
 s{3/2,3/2}          |  s{(3,3,5/2)}[англ.]     |  sr{5,5/2}[англ.]      |  s{(3,5,5/3)}[англ.]     |  sr{5/2,3}[англ.]        |
 sr{5/3,5}[англ.]        |  s{(5/2,5/3,3)}[англ.]     |  sr{5/3,3}[англ.]        |  s{(3/2,3/2,5/2)}[англ.] |  s{3/2,5/3}      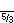  |
Плосконосые многогранники и соты Коксетера в пространствах высокой размерности
В общем случае правильные 4-мерные многогранники с символом Шлефли, и диаграммой Коксетера 





 имеет плосконосую форму с расширенным символом Шлефли и диаграммой
имеет плосконосую форму с расширенным символом Шлефли и диаграммой 





 .
.
Полноусечённый многогранник = r{p,q,r}, and 





 has snub symbol = sr{p,q,r}, and
has snub symbol = sr{p,q,r}, and 





 .
.
Примеры

Существует лишь один однородный плосконосый многогранник в 4-мерном пространстве, Плосконосый 24-ячейник[англ.]. Правильный двадцатичетырёхъячейник имеет символ Шлефли, и диаграмму Коксетера 





 , а плосконосый 24-ячейник представляется символом и диаграммой диаграмма Коксетера
, а плосконосый 24-ячейник представляется символом и диаграммой диаграмма Коксетера 





 . Он имеет также построение с более низкой симметрией с индексом 6 как или s{31,1,1} и
. Он имеет также построение с более низкой симметрией с индексом 6 как или s{31,1,1} и 


 , и симметрией с индексом 3 как или sr{3,3,4},
, и симметрией с индексом 3 как или sr{3,3,4}, 





 или
или 



 .
.
Связанные Плосконосые 24-ячейные соты[англ.] модно рассматривать как или s{3,4,3,3}, 







 , тело с более низкой симметрией как или sr{3,3,4,3} (
, тело с более низкой симметрией как или sr{3,3,4,3} (







 или
или 





 ), и с наименьшей симметрией как или s{31,1,1,1} (
), и с наименьшей симметрией как или s{31,1,1,1} (



 ).
).
Евклидовыми сотами являются альтернированные шестиугольные пластинчатые соты[англ.], s{2,6,3} (





 ) или sr{2,3,6} (
) или sr{2,3,6} (





 ) или sr{2,3[3]} (
) или sr{2,3[3]} (



 ).
).
Другими евклидовыми (равнорёберными) сотами являются альтернированные квадратные пластинчатые соты[англ.] s{2,4,4} (and 





 ) или sr{2,41,1} (
) или sr{2,41,1} (



 ):
):
Единственными однородными плосконосыми гиперболическими сотами являются плосконосые шестиугольные мозаичные соты, s{3,6,3} и 





 , которые можно построить также как Альтернированные шестиугольные мозаичные соты[англ.], h{6,3,3},
, которые можно построить также как Альтернированные шестиугольные мозаичные соты[англ.], h{6,3,3}, 





 . It is also constructed as s{3[3,3]} and
. It is also constructed as s{3[3,3]} and 

 .
.
Другими гиперболическими (равнорёберными) сотами являются плосконосые октаэдральные соты порядка 4[англ.], s{3,4,4} и 





 .
.
См. также
| Основа | Усечение | Полное усечение | Глубокое усечение[англ.] | Двойствен- ность | Растяжение | Всеусечение[англ.] | Альтернация[англ.] | ||
|---|---|---|---|---|---|---|---|---|---|
     |      |      |      |      |      |      |      |      |      |
 |  |  |  |  |  |  |  |  |  |
| t0{p, q} {p, q} | t01{p,q}[англ.] t{p, q} | t1{p,q} r{p, q} | t12{p,q}[англ.] 2t{p, q} | t2{p, q} 2r{p, q} | t02{p,q}[англ.] rr{p, q} | t012{p,q}[англ.] tr{p, q} | ht0{p,q}[англ.] h{q, p} | ht12{p,q} s{q, p} | ht012{p,q} sr{p, q} |
Примечания
- ↑ Kepler, Harmonices Mundi, 1619
- ↑ Conway, 2008, с. 287.
- ↑ Conway, 2008, с. 401.
Литература
- H. S. M. Coxeter, M. S. Longuet-Higgins, J. C. P. Miller. Uniform polyhedra // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — The Royal Society, 1954. — Т. 246, вып. 916. — С. 401–450. — ISSN 0080-4614. — doi:10.1098/rsta.1954.0003. — JSTOR 91532.
- Coxeter, H.S.M. 8.6 Partial truncation, or alternation // Regular Polytopes. — 3rd. — 1973. — С. 154–156. — ISBN 0-486-61480-8.
- Coxeter. Tables I and II: Regular polytopes and honeycombs // Regular Polytopes[англ.]. — 3rd. ed.. — Dover Publications, 1973. — С. 154–156. — ISBN 0-486-61480-8.
- H.S.M. Coxeter. Kaleidoscopes: Selected Writings of H.S.M. Coxeter / F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6.
- (Paper 17) Coxeter, The Evolution of Coxeter–Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233–248]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- H.S.M. Coxeter. Chapter 3: Wythoff's Construction for Uniform Polytopes // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — ISBN 0-486-40919-8.
- N.W. Johnson. Uniform Polytopes. — 1991. — (Manuscript).
- N.W. Johnson. The Theory of Uniform Polytopes and Honeycombs. — University of Toronto, 1966. — (Ph.D. Dissertation).
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5.
- Weisstein, Eric W. Snubification (англ.) на сайте Wolfram MathWorld.
- Richard Klitzing. Snubs, alternated facetings, and Stott–Coxeter–Dynkin diagrams // Symmetry: Culture and Science. — 2010. — Т. 21, вып. 4. — С. 329–344.