Phương pháp nhân tử Lagrange

Hình 1: Tìm x và y để có f(x, y) lớn nhất dưới điều kiện (vẽ bởi màu đỏ) g(x, y) = c.
Hình 2: Đường đồng mức tương ứng của Hình 1. Đường đỏ thể hiện giới hạn g(x, y) = c. Các đường xanh là những đường đồng mức f(x, y). Tại điểm mà đường đỏ tiếp xúc tiếp tuyến với đường đồng mức màu xanh là nghiệm phải tìm. Vì d1 > d2, nghiệm là giá trị cực đại địa phương của f(x, y).

Trong ngành tối ưu hóa, phương pháp nhân tử Lagrange (đặt theo tên của nhà toán học Joseph Louis Lagrange[1]) là một phương pháp để tìm cực tiểu hoặc cực đại địa phương của một hàm số chịu các điều kiện giới hạn.

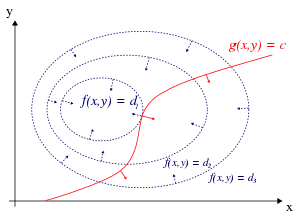
Ví dụ (xem Hình 1), xét bài toán tối ưu hóa

tìm cực đại của hàm f(x, y)
chịu điều kiện giới hạn g(x, y) = 0.

Chúng ta cần f và g đều phải thỏa mãn là chúng liên tục tại đạo hàm riêng bậc nhất của chúng. Đặt một biến mới (λ) gọi là nhân tử Lagrange và nghiên cứu hàm Lagrange (hay Lagrangian) định nghĩa bằng

Λ ( x , y , λ ) = f ( x , y ) + λ ⋅ g ( x , y ) , {\displaystyle \Lambda (x,y,\lambda )=f(x,y)+\lambda \cdot g(x,y),}

với số hạng λ có thể là cộng hoặc trừ. Nếu f(x0, y0) là giá trị cực đại của f(x, y) cho bài toán giới hạn ban đầu, thì tồn tại λ0 sao cho (x0, y0, λ0) là một điểm dừng của hàm Lagrange (điểm dừng là những điểm mà đạo hàm riêng của nó theo Λ bằng 0). Tuy vậy, không phải mọi điểm dừng đều cho tương ứng với một nghiệm của bài toán ban đầu. Do đó, phương pháp nhân tử Lagrange mang lại điều kiện cần cho mục đích tối ưu hóa trong các bài toán giới hạn.[2][3][4][5][6] Điều kiện đủ cho giá trị cực đại và cực tiểu cũng phải thỏa mãn.

Tham khảo

  1. ^ “Mécanique analytique: Lagrange, J. L. (Joseph Louis), 1736-1813: Free Download & Streaming: Internet Archive”. Internet Archive. Truy cập 14 tháng 9 năm 2015.
  2. ^ Bertsekas, Dimitri P. (1999). Nonlinear Programming . Cambridge, MA.: Athena Scientific. ISBN 1-886529-00-0.
  3. ^ Vapnyarskii, I.B. (2001), “Lagrange multipliers”, trong Hazewinkel, Michiel (biên tập), Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4.
  4. ^
    • Lasdon, Leon S. (1970). Optimization theory for large systems. Macmillan series in operations research. New York: The Macmillan Company. tr. xi+523. MR 0337317.
    • Lasdon, Leon S. (2002). Optimization theory for large systems . Mineola, New York: Dover Publications, Inc. tr. xiii+523. MR 1888251.
  5. ^ Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). “XII Abstract duality for practitioners”. Convex analysis and minimization algorithms, Volume II: Advanced theory and bundle methods. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 306. Berlin: Springer-Verlag. tr. 136–193 (and Bibliographical comments on pp. 334–335). ISBN 3-540-56852-2. MR 1295240.
  6. ^ Lemaréchal, Claude (2001). “Lagrangian relaxation”. Trong Michael Jünger and Denis Naddef (biên tập). Computational combinatorial optimization: Papers from the Spring School held in Schloß Dagstuhl, May 15–19, 2000. Lecture Notes in Computer Science. 2241. Berlin: Springer-Verlag. tr. 112–156. doi:10.1007/3-540-45586-8_4. ISBN 3-540-42877-1. MR 1900016.

Liên kết ngoài

Exposition

  • Conceptual introduction (plus a brief discussion of Lagrange multipliers in the calculus of variations as used in physics)
  • Lagrange Multipliers for Quadratic Forms With Linear Constraints by Kenneth H. Carpenter

For additional text and interactive applets

  • Simple explanation with an example of governments using taxes as Lagrange multipliers
  • Lagrange Multipliers without Permanent Scarring Explanation with focus on the intuition by Dan Klein
  • Geometric Representation of Method of Lagrange Multipliers Provides compelling insight in 2 dimensions that at a minimizing point, the direction of steepest descent must be perpendicular to the tangent of the constraint curve at that point. [Needs InternetExplorer/Firefox/Safari] Mathematica demonstration by Shashi Sathyanarayana
  • Applet
  • Video Lecture of Lagrange Multipliers
  • MIT OpenCourseware Video Lecture on Lagrange Multipliers from Multivariable Calculus course
  • Slides accompanying Bertsekas's nonlinear optimization text, with details on Lagrange multipliers (lectures 11 and 12)
  • Geometric idea behind Lagrange multipliers
Hình tượng sơ khai Bài viết liên quan đến toán học này vẫn còn sơ khai. Bạn có thể giúp Wikipedia mở rộng nội dung để bài được hoàn chỉnh hơn.
  • x
  • t
  • s