ガリレイ変換
ガリレイ変換(ガリレイへんかん、英: Galilean transformation)とはある慣性系における物理現象の記述を別の慣性系での記述に変換するための座標変換の方法の一つである。ニュートンの運動方程式を不変に保つため、ガリレイ変換の前後でニュートン力学の法則は不変に保たれる。対して相対論的運動方程式やマクスウェルの方程式は不変に保たないため、光速に近い速度の関わる物理現象に適用すると現実の物理法則と乖離する。なお相対論的効果も考慮した変換はローレンツ変換を参照。
概要
座標系 x,y,z,t で表される慣性系 S に対して、座標系 x′,y′,z′,t′ で表される慣性系 S′ が速度 Vx で相対運動しているとする。ただし運動方向を x 軸と x′ 軸の正方向とし、y 軸と y′ 軸およびz 軸と z′ 軸の方向も一致させる。このとき慣性系 S から慣性系 S′ へのガリレイ変換は次のように定義される。
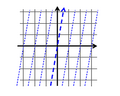
ここで x-t 座標と x′-t′ 座標のみを図示すれば次のようになる。
- 図1.座標格子のガリレイ変換
- 図2.ガリレイ変換。左図は慣性系を直交座標で示し、右図は慣性系を直交座標で示す。
上記の式を時間微分すると、y, z は時間に対して一定なので
となる。
このように、慣性系間をガリレイ変換で変換できるという主張は速度合成則が単純な足し算で記述されるという主張を含むのである。
解説
ガリレイ変換がどのようなものかを理解するために次のような例を考える。
西向きに時速 30 km で走行する列車にピッチングマシーンとそれを操作する人(A とする)が列車上の同じ場所にとどまって乗っている。また、列車の外に立っている人(B とする)がいる。ここで西向きを x 軸、鉛直方向上向きを z 軸、これらに垂直な向き(ここでは右手系を採用することにするので南向き)を y 軸にとる。
時刻 に A がいた位置を原点ととることにする。大地に固定された慣性系(すなわちBの視点)から見ると A の位置は では , , であり、任意の時刻においては
である。一方列車とともに移動する慣性系から見ると A はずっと動かないから A の座標は恒等的に , , である。
さてここで、具体例として A がピッチングマシーンを時速 100 km の設定にして列車の進行方向にボールを発射したとする。A の視点から見ると A 自身は列車の中の一所にとどまっておりボールは時速 100 km で西向きに飛んでいったように見える。しかしここで大地に固定された慣性系(すなわちBの視点)からこの現象を見るとどうなるだろう。ボールはピッチングマシーンの設定速度 100 km に列車の速度 30 km をくわえた 130 km で西向きに飛んでいるように見えるのでは有るまいか?
以上の記述はガリレイ変換が成立する場合には正しい。上記のような状況では実際の観測結果とガリレイ変換の主張は一致するであろう。相対論的な効果によるずれはこの場合非常にわずか(今の場合、 0.000000000001 % 程度)であり、空気抵抗・万有引力その他の外乱要因よりもはるかに小さいため、どんなに精密な測定をしても検出することは不可能である。
しかし、より高い速度では相対論的効果によるずれがより大きくなり、観測にもかかる。一般的に相対論的効果があらわに現れるのは概ね光速の 10 % よりも速い場合である(速度が光速の 10 % の時、相対論的効果は 0.5 % 程度現れる)。
ガリレイの相対性原理
一般に相対性原理というとアインシュタインのものが有名であるが、相対性原理は他にもある。それはガリレイ変換と関係のあるガリレイの相対性原理である。
相対性原理とはどのような慣性系においても同じ物理法則が成り立つという主張である。ガリレイの相対性原理はガリレイ変換によって変換するあらゆる慣性系において物理法則が不変であるという主張である。
ニュートン力学の運動方程式(のベクトル表現)
には座標の二回微分(=速度の一回微分つまり加速度。式中における )しかでてこないので、ガリレイ変換をしても運動方程式には影響しない。つまりガリレイ変換に対して式の形が変わらない。このようなことをさして「ニュートン力学はガリレイ変換に関して共変な理論である」という。ニュートン力学はガリレイの相対性原理の要請を満たす。
しかし電磁気学のマクスウェルの方程式は光速度をあらわに含むのでガリレイ変換に対して不変ではない(光速度に定数を足すと式の形が変わってしまう)。当初はこれを「マクスウェルの方程式は絶対静止座標系[注釈 1]においてのみ成り立つ」と解釈し、絶対静止座標系以外の慣性系では、ガリレイ変換されたマクスウェルの方程式が成り立つと解釈されていた。しかし、絶対静止座標系を見出すのに十分な精度の実験(マイケルソン・モーレーの実験等)が行われても、慣性系の違いによるガリレイ変換の効果は観測されなかった。
この実験結果を説明するため、絶対静止座標系からの変換がガリレイ変換ではないとされ、電磁気学が共変になるような変換であるローレンツ変換が考えだされた。さらに、絶対静止座標の仮定を廃し、ローレンツ変換によって変換するあらゆる慣性系で物理法則が不変であるというアインシュタインの特殊相対性原理[注釈 2]から特殊相対性理論が生み出された。ローレンツ変換において、光速に対して慣性系間の相対速度を微小として近似したものが、ガリレイ変換になる。
脚注
注釈
関連項目
| |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 特殊 相対論 |
|  | |||||||||||
| 一般 相対論 |
| ||||||||||||
| 科学者 | |||||||||||||
| | |||||||||||||