ファントホッフの式

ファントホッフの式（ファントホッフのしき、英: van 't Hoff equation）は、化学反応の過程に対する標準エンタルピー変化ΔH^⊖を考慮して、化学反応の平衡定数K_eqにおける変化と温度Tにおける変化を結び付ける式であり、オランダの化学者ヤコブス・ヘンリクス・ファント・ホッフによる1884年の著作『Études de dynamique chimique（動的化学における諸研究）』において提唱された^[1]。この式はVukančić–Vuković式と呼ばれることもある^[2][3][4]。

ファントホッフ式は熱力学系における状態関数の変化を探るために広く利用されてきた。この式から導かれるファントホッフ・プロットは化学反応のエンタルピー（全エネルギー）変化、ならびにエントロピー（到達可能な微視的状態（英語版）の数）変化を見積るうえで特に有効である。

式

標準状態下

標準状態下でのファントホッフ式は

${\displaystyle {\frac {d}{dT}}\ln K_{\mathrm {eq} }={\frac {\Delta H^{\ominus }}{RT^{2}}}}$

である^[5][6]。上式においてlnは自然対数で、Rは理想気体定数である。この式はいかなる温度においても厳密である。実際上、この式は反応エンタルピーΔHが一定であるという仮定の下で2つの温度間で積分されることが多い。現実にはΔHおよび反応エントロピーΔSはほとんどの過程に対して温度によって変動するため^[7]、積分された式は近似でしかない。

積分された式の主用途は、ある温度域にわたる一定の標準エンタルピー変化を仮定し、新しい絶対温度での新しい平衡定数を見積ることである。

積分された式を得るためには、最初にファントホッフ式を

${\displaystyle {\frac {d\ln K_{\mathrm {eq} }}{d(1/T)}}=-{\frac {\Delta H^{\ominus }}{R}}.}$

と書き直すのが便利である^[5]。次に温度T₁ とT₂との間の定積分は

${\displaystyle \ln {\frac {K_{2}}{K_{1}}}=-{\frac {\Delta H^{\ominus }}{R}}\left({\frac {1}{T_{2}}}-{\frac {1}{T_{1}}}\right)}$

である。この式において、K₁は絶対温度T₁での平衡定数、K₂は絶対温度T₂での平衡定数である。

熱力学からの発展

ギブズの自由エネルギー（英語版）の定義

${\displaystyle \Delta G^{\ominus }=\Delta H^{\ominus }-T\Delta S^{\ominus }}$

（Sは系のエントロピー）とギブズの自由エネルギー等温式^[8]

${\displaystyle \Delta G^{\ominus }=-RT\ln K_{\mathrm {eq} }}$

を組み合わせると、以下の式が得られる。

${\displaystyle \ln K_{\mathrm {eq} }=-{\frac {\Delta H^{\ominus }}{RT}}+{\frac {\Delta S^{\ominus }}{R}}}$

変数Tに関するこの式の微分によりファントホッフ式が得られる。

ΔH^⊖およびΔS^⊖が一定であるという条件で、上式は 1/Tの線形関数としてのln Kを与え、ゆえにファントホッフ式の「線形形式」と呼ばれる。したがって、標準エンタルピーおよびエントロピー変化が実質的に一定であるほど温度範囲が小さい時、温度の逆数に対するこの式の自然対数のプロットは直線を与える。この直線の傾きに気体定数Rを掛けることで反応の標準エンタルピー変化が得られ、切片にRを掛けることで標準エントロピー変化が得られる。

ファントホッフの等温式

ギブズの自由エネルギーは熱力学系の温度と圧力と共に変化する。ファントホッフの等温式は、一定の温度での非標準状態反応に対するギブズの自由エネルギーを決定するために使うことができる^[9]。

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G+RT\ln Q_{\mathrm {r} }}$

上式において、Δ_rGは反応に対するギブズの自由エネルギー、 Q_rは反応商（英語版）である。反応が化学平衡にある時、Q_r = K_eqである。ファントホッフの等温式は平衡反応のずれを見積る助けとなる。Δ_rG < 0の時、反応は順方向へ動く。Δ_rG > 0の時、反応は逆方向へ動く。

ファントホッフ・プロット

可逆反応について、様々な温度で平衡定数を測定することができる。このデータを、y-軸にln K_eq、x軸上に1/Tを取ったグラフ上にプロットする。このデータは線形関係を持っているはずであり、この関係についての方程式はファントホッフ方程式の線形形式を使用してデータを当て嵌めることによって見つけることができる。

${\displaystyle \ln K_{\mathrm {eq} }=-{\frac {\Delta H^{\ominus }}{RT}}+{\frac {\Delta S^{\ominus }}{R}}}$

このグラフはファントホッフ・プロットと呼ばれ、化学反応のエンタルピーとエントロピーを見積るために広く使われている。このプロットから、−ΔH/RおよびΔS/Rはそれぞれ線形当て嵌めの傾きおよび切片である。

異なる温度で平衡定数K_eqを測定することによって、ファントホッフプロットは温度が変化した時の反応を評価するために使うことができる^[10][11]。ファントホッフから傾きと切片を知ることで、反応のエンタルピーとエントロピーを以下の式によって容易に得ることができる。

${\displaystyle {\begin{aligned}\Delta H&=-R\times {\text{slope}},\\\Delta S&=R\times {\text{intercept}}\end{aligned}}}$

ファントホッフ・プロットは、化学反応のエンタルピーを定性的にも定量的にも迅速に求めるために使用できる。エンタルピーの変化は正または負のどちらかであり、ファントホッフ・プロットの2つの主要な形式となる。

吸熱反応

吸熱反応では、熱が吸収されて正味のエンタルピー変化が正の値になる。したがって、プロットの傾きの定義

${\displaystyle {\text{slope}}=-{\frac {\Delta H}{R}}}$

に従えば、吸熱反応では、ΔH > 0（かつ気体定数R > 0）であるため、

${\displaystyle {\text{slope}}=-{\frac {\Delta H}{R}}<0}$

となる。このように、吸熱反応の場合、ファントホッフ・プロットは、常に負の傾きを持つはずである。

発熱反応

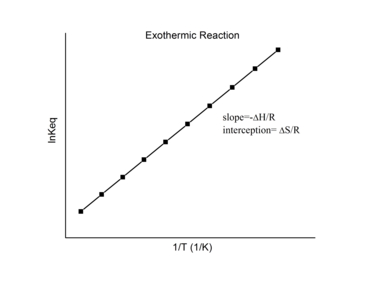
発熱反応では、熱が放出されて正味のエンタルピー変化が負の値になる。したがって、プロットの傾きの定義

${\displaystyle {\text{slope}}=-{\frac {\Delta H}{R}}}$

に従えば、発熱反応では、ΔH < 0 であるため、

${\displaystyle {\text{slope}}=-{\frac {\Delta H}{R}}>0}$

となる。このように、発熱反応の場合、ファントホッフ・プロットは、常に正の傾きを持つはずである。

誤差の伝播

ΔG^⊖ = −RT ln K = ΔH^⊖ − TΔS^⊖という事実を利用すると、ΔH^⊖の値を得るためには、Kを2回測定すれば十分であるように見える。

${\displaystyle \Delta H^{\ominus }=R{\frac {\ln K_{1}-\ln K_{2}}{1/T_{2}-1/T_{1}}}}$

上式において、K₁およびK₂はそれぞれ温度T₁およびT₂において得られる平衡定数の値である。このようにして得られたΔH^⊖値の精度は、平衡定数の値の精度に大きく依存する。典型的な温度の対は、25 °Cと35 °C（298 Kと308 K）かもしれない。これらの温度では、

${\displaystyle {\frac {1}{T_{2}}}-{\frac {1}{T_{1}}}={\frac {1}{298~\mathrm {K} }}-{\frac {1}{308~\mathrm {K} }}=1.1\times 10^{-4}{\text{ K}}}$

である。この値を使うと

${\displaystyle \Delta H^{\ominus }\approx 76\left(\ln K_{1}-\ln K_{2}\right){\text{ kJ/mol}}}$

となる。

さて、誤差の伝播（英語版）は、ΔH^⊖の誤差が (ln K₁ − ln K₂) の誤差の約76 kJ/mol倍、またはln K値の誤差の約110 kJ/mol倍になることを示している。例えば、各ln Kの誤差がσ ≈ 0.05であると仮定する。ΔH^⊖の誤差は約5 kJ/molになる。このように、個々の安定性定数が精度よく決定されたにもかかわらず、このようにして計算されたエンタルピーには大きな誤差が生じることになる。

そうすると、エントロピーはΔS^⊖ = 1/T(ΔH^⊖ + RT ln K)から得られることになる。この式では、第2項の誤差は第1項の誤差に比べて無視できる程度である。拡大率は76 kJ/mol ÷ 298 Kなので、対数での誤差が0.05の場合、ΔS^⊖の誤差は17 J/(K mol)のオーダーとなる。

平衡定数が3つ以上の温度で測定された場合、ΔH^⊖の値は直線的なフィッティングによって得られる。この場合、標準エンタルピーの誤差は幾分小さくなるが、それでもかなりの程度にまで拡大される。

ファントホッフ・プロットの応用

ファントホッフ解析

生物学研究において、ファントホッフ・プロットはファントホッフ解析とも呼ばれる^[12]。これは、反応において有利な生成物を決定するのに最も効果的である。

In biological research, the van't Hoff plot is also called van't Hoff analysis. It is most effective in determining the favored product in a reaction.

ある反応で2つの生成物bとcが形成されるとする。

a A + d D → b B,

a A + d D → c C

この場合、K_eqは平衡定数ではなく、BとCの比として定義することができる。

とするとB/C > 1の場合、Bが有利な生成物であり、ファントホッフ・プロットのデータは正の領域に存在する。

B/C < 1の場合、Cが有利な生成物であり、ファントホッフ・プロットのデータは負の領域に存在する。

この情報を使用して、ファントホッフ解析は、有利な生成物に最適な温度を決定するのに役立つ。

2010年には、水がアミノ酸プロリンのC末端とN末端のどちらと優先的に水素結合を形成するかを決定するためにファントホッフ・プロットが使われた^[13]。様々な温度で各反応の平衡定数を求め、ファントホッフ・プロットを作成した。この解析により、エンタルピー的には水はC末端との水素結合を好むが、エントロピー的にはN末端との水素結合を好むことが示された。具体的には、C末端の水素結合が4.2–6.4 kJ/mol有利であることがわかった。N末端の水素結合は31–43 J/(K mol) 有利であった。

このデータだけでは、水がどの部位に優先的に水素結合するかを結論づけることができなかったため、追加の実験が行われた。その結果、低温では、エンタルピー的に有利な化学種であるC末端に水素結合した水が好まれることがわかった。より高い温度では、エントロピー的に好まれる種であるN末端に水素結合した水が好まれることがわかった。

反応機構解析

化学反応は、温度によって異なる反応機構を経ることがある^[14]。

この場合、2つ以上の線形フィットを持つファントホッフ・プロットを利用することができる。それぞれの線形フィットは、異なる勾配と切片を持ち、それぞれの異なる機構のエンタルピーとエントロピーの異なる変化を示す。ファントホッフ・プロットは、異なる温度下での各機構のエンタルピーとエントロピーの変化、および有利な機構を見つけるために使用することができる。

${\displaystyle {\begin{aligned}\Delta H_{1}&=-R\times {\text{slope}}_{1},&\Delta S_{1}&=R\times {\text{intercept}}_{1};\\[5pt]\Delta H_{2}&=-R\times {\text{slope}}_{2},&\Delta S_{2}&=R\times {\text{intercept}}_{2}\end{aligned}}}$

図示例では、高温では機構1、低温では機構2を経て反応が進行する。

温度依存性

ファントホッフ・プロットは、エンタルピーとエントロピーが温度変化に伴って一定であるという暗黙の前提に基づいた線形プロットである。しかし、ある場合には、エンタルピーとエントロピーは温度によって劇的に変化する。一次近似では、2つの異なる反応生成物が異なる熱容量を持つと仮定します。この仮定を組み込むと、温度の関数としての平衡定数の式中に追加項c/T²が得られる。多項式当て嵌めは、反応の標準エンタルピーが一定でないことを示すデータを分析するために使用することができる^[15]。

${\displaystyle \ln K_{\mathrm {eq} }=a+{\frac {b}{T}}+{\frac {c}{T^{2}}},}$

上式において

${\displaystyle {\begin{aligned}\Delta H&=-R\left(b+{\frac {2c}{T}}\right),\\\Delta S&=R\left(a-{\frac {c}{T^{2}}}\right)\end{aligned}}}$

である。

このように、反応のエンタルピーとエントロピーは、温度依存性がある場合でも、特定の温度で決定することができる。

界面活性剤の自己組織化

ファントホッフの関係式は、臨界ミセル濃度（CMC）の温度依存性からの界面活性剤のミセル化エンタルピーΔH⊖
mの決定に特に有用である。

${\displaystyle {\frac {d}{dT}}\ln \mathrm {CMC} ={\frac {\Delta H_{\mathrm {m} }^{\ominus }}{RT^{2}}}}$

しかし、会合数（英語版）も温度依存性があるとこの関係は妥当性を失うので、代わりに次のような関係を用いるべきである^[16]。

${\displaystyle RT^{2}\left({\frac {\partial }{\partial T}}\ln \mathrm {CMC} \right)_{P}=-\Delta H_{\mathrm {m} }^{\ominus }(N)+T\left({\frac {\partial }{\partial N}}\left(G_{N+1}-G_{N}\right)\right)_{T,P}\left({\frac {\partial N}{\partial T}}\right)_{P}}$

上式において、G_{N + 1}およびG_Nはそれぞれ会合数N + 1およびNを持つミセル中の界面活性剤の自由エネルギーである。この効果は、非イオン性エトキシル化界面活性剤（英語版）^[17]やポリオキシプロピレン・ポリオキシエチレンブロック共重合体（ポロキサマー）と特に関連している^[18]。この拡張式は、示差走査熱量測定サーモグラムから自己組織化ミセルの会合数を抽出するために利用できる^[19]。

出典

関連項目

• クラウジウス・クラペイロンの式
• ファントホッフ係数（英語版） (i)
• ギブズ-ヘルムホルツの式
• 溶解平衡（英語版）