包除原理

包除原理（ほうじょげんり、英: Inclusion-exclusion principle, principle of inclusion and exclusion, Principle of inclusion-exclusion, PIE）あるいは包含と排除の原理とは、数え上げ組合せ論における基本的な結果のひとつ。特別な場合には「有限集合 A と B の和集合に属する元の数を計算するには、まずそれぞれに属する元の数 |A| と |B| を足しあわせた後、それらの共通部分に属する元の数 |A ∩ B| を引き去ればよい」というものである。つまり単に数え上げた後で重複を取り除くことに相当する。

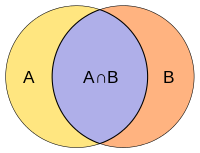
以上の2つの有限集合 A, B に対する包除原理は次のように表せる。

{\begin{aligned}\left|A\cup B\right|=&\left|A\right|+\left|B\right|-\left|A\cap B\right|\\\end{aligned}}

同様に、3つの有限集合 A, B, C に対する包除原理は次のように表せる。

{\begin{aligned}\left|A\cup B\cup C\right|=&\left|A\right|+\left|B\right|+\left|C\right|\\&\quad -\left|A\cap B\right|-\left|B\cap C\right|-\left|C\cap A\right|\\&\qquad +\left|A\cap B\cap C\right|\end{aligned}}

一般に、 n 個の有限集合 A₁, ..., A_n が与えられたとき、その和集合に属する元の数は

{\begin{aligned}\left\vert \bigcup _{i=1}^{n}A_{i}\right\vert &=\sum _{k=1}^{n}(-1)^{k-1}\!\sum _{J\subseteq [n],\ \vert J\vert =k}\left\vert \bigcap _{j\in J}A_{j}\right\vert \\&=\sum _{i}\left|A_{i}\right|-\sum _{i<j}\left|A_{i}\cap A_{j}\right|+\cdots +(-1)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|\end{aligned}}

と表せる^[1]^[2]。ただし、ここで [n] = {1, 2, …, n} とした。

この原理の名称は、あらゆるものを「含め」、その後で「取り除いて」補正をするという考え方に基づいていることからきている。n > 2 のとき、共通部分の補正項を計算するのが非常に困難になることもある。また、公式には符号が交互にあらわれる。

この公式はアブラーム・ド・モアブルによるものと考えられているが、ジェームス・ジョセフ・シルベスターまたはアンリ・ポアンカレによるとも言われる。

証明

包除原理を一般に証明するため、X を A₁, ..., A_n の上位集合とする。公式はまず恒等式

1_{\bigcup A_{i}}=\sum _{i}1_{A_{i}}-\sum _{i<j}1_{A_{i}\cap A_{j}}+\cdots +(-1)^{n-1}1_{\bigcap A_{i}}

を指示関数の変形でもとめ、全ての x ∈ X について足しあわせることで示される。

その他の形

この原理は時に以下のような形で表される^[3]。有限集合 S のべき集合 2^S 上で定義された関数 f, g が

g(A)=\sum _{B\subseteq A}f(B)

を満たすならば、

f(A)=\sum _{B\subseteq A}(-1)^{\left|A\setminus B\right|}g(B).

この形は半順序集合 2^S の隣接代数におけるメビウスの反転公式となる。

また、包除原理は確率においても以下のように用いられる。

\Pr \left(\bigcup _{i}A_{i}\right)=\sum _{i}\Pr \left(A_{i}\right)-\sum _{i<j}\Pr \left(A_{i}\cap A_{j}\right)+\cdots +(-1)^{n-1}\Pr \left(\bigcap _{i}A_{i}\right)

ボンフェローニの不等式によれば、この公式の始めの k 項の和は左辺の上界と下界を交互にとる^[4]：

{\begin{aligned}\Pr \left(\bigcup _{i}A_{i}\right)&\leq \sum _{i}\Pr \left(A_{i}\right),\\\Pr \left(\bigcup _{i}A_{i}\right)&\geq \sum _{i}\Pr \left(A_{i}\right)-\sum _{i<j}\Pr \left(A_{i}\cap A_{j}\right),\\\Pr \left(\bigcup _{i}A_{i}\right)&\leq \sum _{i}\Pr \left(A_{i}\right)-\sum _{i<j}\Pr \left(A_{i}\cap A_{j}\right)+\sum _{i<j<k}\Pr \left(A_{i}\cap A_{j}\cap A_{k}\right),\\&\vdots \end{aligned}}

このことは公式全体が扱いにくい場合に利用される。

応用

おそらく、包除原理のもっともよく知られている応用は、組み合わせ問題における有限集合の攪乱(derangement)に対するものであろう。集合Aの攪乱とはAから自分自身への全単射であって不動点を持たないもののことである。包除原理によって、Aの基数（要素数）をnとしたときの攪乱の数が

\left[{\frac {n!}{e}}\right]

となることを示せる。ここで[x]はもっとも近い整数をあたえる関数(nearest integer function)を表す。

これはnのsubfactorialとしても知られ、 $!n$ と表す。これはまた、全ての全単射に等しい確率が与えられた場合、無作為に選ばれた全単射が攪乱となっている確率がnの増加に従い、1/e に素早く近づくことを示している。

この原理によって理論的な公式を求める場合（特にエラトステネスの篩を用いる素数の数え上げ）、誤差評価が困難であるため有効な公式が得られないことが多い。これは、各項が個別には正確に求められてもそれらの相殺の様子を一般的に定式化することが難しい上に、和の項数が非常に多くなってしまうためである。数論において、ヴィーゴ・ブルンはこのような困難を部分的に克服する方法を見出し、これは現代的な篩の理論の端緒となった。ただし、この理論を用いてもたいてい、厳密な公式はもとより漸近公式さえ得られるのもまれで、したがってふるい落とされた集合の大きさの評価を与えるにとどまる。

共通部分の計算

包除原理とド・モルガンの法則とを合わせることで、共通部分の要素数を計算できる。 $A$ を普遍集合、各 $i$ について $A_{i}\subseteq A$ とし、 ${\overline {A_{i}}}$ が $A$ に関する $A_{i}$ の補集合を表すものとする。このとき

$\left\vert \bigcap _{i=1}^{n}A_{i}\right\vert ={\overline {\left\vert \bigcup _{i=1}^{n}{\overline {A_{i}}}\right\vert }}$

をえる。こうして、共通部分をもとめる問題を和集合をもとめる問題に帰着させることができる。

脚注

^ 数学辞典 2007, 63. 数え上げ理論.
^ 西岡 2013, p. 50, 4.4 包除原理.
^ Gessel & Stanley 1995, p. 1049.
^ Galambos 2001.

参考文献

西岡康夫『数学チュートリアルやさしく語る確率統計』オーム社、2013年。ISBN 978-4-274-21407-3。https://books.google.co.jp/books?id=AUY2AgAAQBAJ。
伏見康治『確率論および統計論』（復刻版再発行）現代工学社、2002年12月10日（原著1942年）。ISBN 978-4-87472-012-7。https://web.archive.org/web/20130503002149/http://ebsa.ism.ac.jp/ebooks/ebook/204。
日本数学会『数学辞典』（第4版）岩波書店、2007年。ISBN 978-4-00-080309-0。
Gessel, Ira M.; Stanley, Richard P. (1995), “Algebraic enumeration”, in Graham, R. L.; Grötschel, M.; Lovász, L., Handbook of Combinatorics, II, MIT Press, pp. 1021–1061, ISBN 978-0-444-88002-4, MR1373655, https://books.google.co.jp/books?id=ZyvpoazU-O0C&pg=PA1021

外部リンク

『包除原理の２通りの証明』 - 高校数学の美しい物語
Weisstein, Eric W. "Inclusion-Exclusion Principle". mathworld.wolfram.com (英語).
Rukova, S.A. (2001), “Inclusion-and-exclusion principle”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Inclusion-and-exclusion_principle
Galambos, J. (2001), “Bonferroni inequalities”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Bonferroni_inequalities