理想気体の状態方程式

熱力学
古典的カルノー熱機関（英語版）
状態（英語版）
過程（英語版）
サイクル
系の特性
注: 斜体は共役変数（英語版）を示す。
状態の関数
過程関数（英語版）
材料特性（英語版）
比熱容量  c = {\displaystyle c=}
T {\displaystyle T} ∂ S {\displaystyle \partial S}
N {\displaystyle N} ∂ T {\displaystyle \partial T}
圧縮率  β = − {\displaystyle \beta =-}
1 {\displaystyle 1} ∂ V {\displaystyle \partial V}
V {\displaystyle V} ∂ p {\displaystyle \partial p}
熱膨張  α = {\displaystyle \alpha =}
1 {\displaystyle 1} ∂ V {\displaystyle \partial V}
V {\displaystyle V} ∂ T {\displaystyle \partial T}
方程式（英語版）
  • 歴史
  • 文化
歴史
  • 一般（英語版）
  • 熱（英語版）
  • エントロピー（英語版）
  • 気体の法則
  • 永久機関（英語版）
哲学（英語版）
理論
重要文献
年表
  • 芸術
  • 教育
  • マクスウェルの熱力学的表面（英語版）
  • エネルギー拡散としてのエントロピー（英語版）
  • 表
  • 話
  • 編
  • 歴
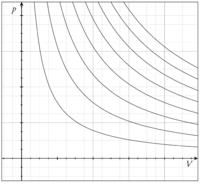
理想気体の等温曲線。温度が一定のいくつかの条件下での圧力 p と体積 V の関係を示す。左下から右上に向かって高温になる。

理想気体の状態方程式（りそうきたいのじょうたいほうていしき、英語: ideal gas law）とは、気体の振る舞いを理想化した状態方程式である。

なお、理想気体は、この状態方程式に従うが、その振る舞いは状態方程式だけでは決まらず、比熱容量の定数性が要求される。

方程式

熱力学温度 T、圧力 p の下で、物質量 n の理想気体が占める体積 V が

p V = n R T {\displaystyle pV=nRT}

で与えられる。ここで係数 R はモル気体定数である。

この式が理想気体の状態方程式であり、ボイルの法則、シャルルの法則（あるいは合わせてボイル＝シャルルの法則）と体積の示量性から導かれる。

実在気体の場合は、気体は近似的にこの方程式に従い、式の有効性は気体の密度が0に近づき（低圧になり）、かつ高温になるにつれて高まる。

何故なら、密度が0に近付けば、分子の運動に際し、お互いがぶつからずに、分子自身の体積が無視できるようになる。また、高温になることによって、分子の運動が高速になり、分子間力（ファンデルワールス力）が無視出来るようになるからである。

諸性質

理想気体の状態方程式から導かれる性質として以下のものがある。これらは比熱容量の定数性が要求されない半理想気体でも成り立つ。

状態方程式の微分から得られる熱膨張係数 α と等温圧縮率 κT は、それぞれ

α = 1 V ( ∂ V ∂ T ) p = 1 T {\displaystyle \alpha ={\frac {1}{V}}\left({\frac {\partial V}{\partial T}}\right)_{p}={\frac {1}{T}}}

κ T = − 1 V ( ∂ V ∂ p ) T = 1 p {\displaystyle \kappa _{T}=-{\frac {1}{V}}\left({\frac {\partial V}{\partial p}}\right)_{T}={\frac {1}{p}}}

である。

熱力学的状態方程式が

( ∂ U ∂ V ) T = T α κ T − p = 0 {\displaystyle \left({\frac {\partial U}{\partial V}}\right)_{T}={\frac {T\alpha }{\kappa _{T}}}-p=0}

( ∂ H ∂ p ) T = T V ( 1 T − α ) = 0 {\displaystyle \left({\frac {\partial H}{\partial p}}\right)_{T}=TV\left({\frac {1}{T}}-\alpha \right)=0}

であり、内部エネルギーやエンタルピーが体積や圧力に依存しない温度だけの関数となる。

ジュール＝トムソン係数が

μ J-T = T V C p ( α − 1 T ) = 0 {\displaystyle \mu _{\text{J-T}}={\frac {TV}{C_{p}}}\left(\alpha -{\frac {1}{T}}\right)=0}

であり、ジュール＝トムソン効果がない。

等圧熱容量と等積熱容量の差が

C p − C V = T V α 2 κ T = n R {\displaystyle C_{p}-C_{V}={\frac {TV\alpha ^{2}}{\kappa _{T}}}=nR}

となる。（マイヤーの関係式）

関連項目