アインシュタイン半径

アインシュタイン半径（アインシュタインはんけい、英: Einstein radius）はアインシュタインリングの半径であり、また一般に重力レンズを特徴付ける角度の一つでもある（重力レンズによってできる像の広がりが典型的にはアインシュタイン半径のオーダーであるため）^[1]。

導出

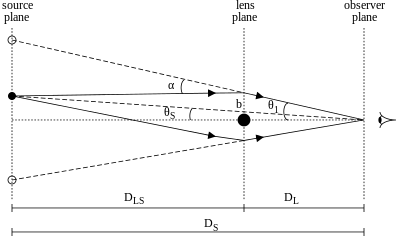
以下の導出では、レンズ源 L の全質量 M はその中心に凝集しているものと考える。質点が作る歪みは計算可能であり、古典的な一般相対性理論のテスト（en:tests of general relativity）の一つでもある。α₁ を質点 M による微小な屈曲角

${\displaystyle \alpha _{1}={\frac {4G}{c^{2}}}{\frac {M}{b_{1}}}}$

とする（シュワルツシルト解を参照）。ここで

b₁ は衝突径数（光線が質量中心へ最接近する距離）。

G は万有引力定数。

c は光速。

角度が微小であるとき（単位はラジアン）、距離 D_L の位置にあるレンズ L へ θ₁ の角度で光線が最接近したとすれば、衝突径数は b₁ = θ₁ D_L となる。屈曲角 α₁ を表す式に代入すると次のように書き直せる。

${\displaystyle \alpha _{1}(\theta _{1})={\frac {4G}{c^{2}}}{\frac {M}{\theta _{1}}}{\frac {1}{D_{\rm {L}}}}}$ ..... (Eqn. 1)

レンズがないときに光源が見える角度を θ_S とし（これは一般には観測不能である）、レンズを通して像が見える角度を θ₁ とする。距離 D_S にある光源面で幾何的に考えると、角度 θ₁ により切り取られる距離は θ_S D_S と α₁ D_LS の和であることがわかるから、レンズ方程式

${\displaystyle \theta _{1}\;D_{\rm {S}}=\theta _{\rm {S}}\;D_{\rm {S}}+\alpha _{1}\;D_{\rm {LS}}}$

が得られ、これを変形すると次式になる。

${\displaystyle \alpha _{1}(\theta _{1})={\frac {D_{\rm {S}}}{D_{\rm {LS}}}}(\theta _{1}-\theta _{\rm {S}})}$ ..... (Eqn. 2)

(eq. 1) と (eq. 2) を等しいと置いて整理すると、次式が得られる。

${\displaystyle \theta _{1}-\theta _{\rm {S}}={\frac {4G}{c^{2}}}\;{\frac {M}{\theta _{1}}}\;{\frac {D_{\rm {LS}}}{D_{\rm {S}}D_{\rm {L}}}}}$

レンズの真後ろにある点光源については θ_S = 0 であり、質点に対するレンズ方程式からはアインシュタイン半径と呼ばれる θ₁ の特性値 θ_E が得られる。θ_S = 0 と置いて θ₁ について解くと

${\displaystyle \theta _{E}=\left({\frac {4GM}{c^{2}}}\;{\frac {D_{\rm {LS}}}{D_{\rm {L}}D_{\rm {S}}}}\right)^{1/2}}$

θ_E はレンズ効果を表す量を作るのに便利な線形尺度で、これを使えばレンズ方程式は次のように書ける。

${\displaystyle \theta _{1}=\theta _{\rm {S}}+{\frac {\theta _{E}^{2}}{\theta _{1}}}}$

アインシュタイン半径に定数を代入すると

${\displaystyle \theta _{E}=\left({\frac {M}{10^{11.09}M_{\bigodot }}}\right)^{1/2}\left({\frac {D_{\rm {L}}D_{\rm {S}}/D_{\rm {LS}}}{\rm {Gpc}}}\right)^{-1/2}{\rm {arcsec}}}$

ここで、質量は太陽質量（M_☉）を単位とし、距離はギガパーセク (Gpc) で表してある。アインシュタイン半径は一般にレンズが光源と観測者の中間点に位置するとき最大になる。

1 ギガパーセク (1 Gpc) ほどの距離にある高密度天体 M_c ≈ 10×10¹⁵ M_☉ に対しては、この半径は 100 arcsec 程度まで大きくなる（重力マクロレンズと呼ばれる）。銀河系の範囲で（例えばD ~ 3 kpc）1 M_☉ 程度の重力マイクロレンズ天体を探索する場合、典型的なアインシュタイン半径は 1/1000秒（milli-arcseconds）のオーダーとなり、結果的にレンズにより分裂した像を観測するのは現在の技術では不可能である。

光がレンズの下側を通って観測者へ到達する場合は同様に考えて

${\displaystyle \theta _{2}\;D_{\rm {S}}=-\;\theta _{\rm {S}}\;D_{\rm {S}}+\alpha _{2}\;D_{\rm {LS}}}$

${\displaystyle \theta _{2}+\theta _{\rm {S}}={\frac {4G}{c^{2}}}\;{\frac {M}{\theta _{2}}}\;{\frac {D_{\rm {LS}}}{D_{\rm {S}}D_{\rm {L}}}}}$

であることがわかり、次式が得られる。

${\displaystyle \theta _{2}=-\;\theta _{\rm {S}}+{\frac {\theta _{E}^{2}}{\theta _{2}}}}$

レンズが質点ではなく広がりを持った質量分布である場合にも、角 α の表現の仕方を変えることでこれまでの議論を一般化でき、それにより像の位置 θ_I(θ_S) が計算できる。屈曲が微小のときはこの関数は1対1対応で、観測される位置での歪みと整合的である（光源の位置を元に戻すことができる）。これを弱い重力レンズ（英語版）（weak lensing）と言う。屈曲が大きい場合、像が多重に現れて元の位置に戻せないようになる。これを強い重力レンズ（英語版）（strong lensing）と言う。質量が広がりを持って分布しているとき、アインシュタインリングができるためは分布が軸対称的でなくてはならないことに注意する。

関連項目

• 重力レンズ

脚注

参考文献

• Chwolson, O (1924). “Über eine mögliche Form fiktiver Doppelsterne”. Astronomische Nachrichten 221 (20): 329–330. Bibcode: 1924AN....221..329C. doi:10.1002/asna.19242212003.  （『見かけ上二重に見える星のありうる形状について』、リングが提案された最初の論文）
• Einstein, Albert (1936). “Lens-like Action of a Star by the Deviation of Light in the Gravitational Field”. Science 84 (2188): 506–507. Bibcode: 1936Sci....84..506E. doi:10.1126/science.84.2188.506. JSTOR 1663250. PMID 17769014.  （アインシュタインリングの有名な論文）
• Renn, Jurgen; Tilman Sauer; John Stachel (1997). “The Origin of Gravitational Lensing: A Postscript to Einstein's 1936 Science paper”. Science 275 (5297): 184–186. Bibcode: 1997Sci...275..184R. doi:10.1126/science.275.5297.184. PMID 8985006. 

表 話 編 歴 アルベルト・アインシュタイン
キャリア	特殊相対性理論 一般相対性理論 E = mc2 ブラウン運動 光電効果 アインシュタイン係数 アインシュタイン模型 等価原理 アインシュタイン方程式 アインシュタイン半径 アインシュタインの関係式 宇宙定数 ボース＝アインシュタイン凝縮 ボース=アインシュタイン分布関数 ボース＝アインシュタイン相関（英語版） アインシュタイン＝カルタン理論（英語版） アインシュタイン＝インフェルト＝ホフマンの方程式（英語版） アインシュタイン＝ド・ハース効果（英語版） EPRパラドックス EBK量子化条件 アインシュタインとボーアのディベート（英語版） 遠隔平行性（英語版） 思考実験（英語版） 成功しなかった研究（英語版） 粒子と波動の二重性 重力波 茶葉のパラドックス
著作物（英語版）	アインシュタインの原論文 奇跡の年 ブラウン運動の理論 (1905) 運動物体の電気力学について (1905) 特殊および一般相対性理論について (1916) わが世界観（英語版） (1949) 私の社会主義（英語版） (1949) ラッセル＝アインシュタイン宣言 (1955)
家族	パウリーネ・コッホ (母) ヘルマン・アインシュタイン (父) マヤ・アインシュタイン (妹) ミレヴァ・マリッチ (1人目の妻) エルザ・アインシュタイン (2人目の妻) リーゼル・アインシュタイン (娘) ハンス・アルベルト・アインシュタイン (息子) エドゥアルト・アインシュタイン (息子) ベルンハルト・アインシュタイン (孫) イヴリン・アインスタイン (孫)
アインシュタイン賞	アルベルト・アインシュタイン賞 アルベルト・アインシュタイン・メダル アルベルト・アインシュタイン平和賞（英語版） アルベルト・アインシュタイン世界科学賞 アインシュタイン賞 (APS) レーザー科学アインシュタイン賞
その他	政治観（英語版） 宗教観（英語版） 家 冷蔵庫 脳 大衆文化におけるアインシュタイン（英語版） アインスタイニウム 受賞・受勲歴（英語版） 由来するもの（英語版） アインシュタイン・ペーパーズ・プロジェクト（英語版） 伝アインシュタイン・エレベーター
カテゴリ