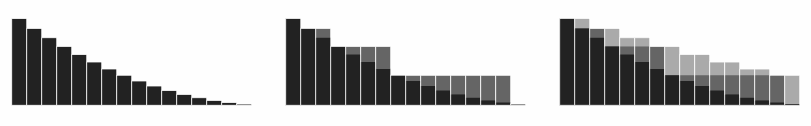コーシーの凝集判定法

下記テーマに関する記事の一部
解析学
基本定理 関数の極限 連続性 平均値の定理
微分法 定義 導関数 (一般化（英語版）) 微分 無限小 関数の 全 概念 微分の記法 二階導関数 三階導関数（英語版） 変数変換（英語版） 陰関数の微分 Related rates（英語版） テイラーの定理 法則と恒等式（英語版） 和（英語版） 積 合成 冪（英語版） 商 一般ライプニッツ ファー・ディ・ブルーノの公式（英語版）
積分法 積分一覧 定義 不定積分 積分 (広義) リーマン積分 ルベーグ積分 線積分 複素線積分 道具 部分 Discs（英語版） 円殻（バウムクーヘン） 置換 三角置換（英語版） 部分分数（英語版） 順序（英語版） 漸化式
級数 幾何 (算術幾何) 調和 交代 冪 二項 テイラー 収束判定法（英語版） 項の極限（項判定法）（英語版） 比 冪根 積分 比較 極限比較（英語版） 交代級数（英語版） 凝集 ディリクレ アーベル（英語版）
ベクトル 勾配 発散 回転 ラプラシアン 方向微分 公式（英語版） 定理 発散 勾配（英語版） グリーン ケルビン・ストークス
多変数 形式と枠組み 行列（英語版） テンソル 外 幾何学的（英語版） 定義 偏微分 多重積分 線積分 面積分 体積分 ヤコビアン ヘッセ行列
特殊化 分数階微積分 解析接続 マリアヴァン（英語版） 確率（英語版） 変分
その他 解析学記号
表 話 編 歴

数学において、コーシーの凝集判定法（コーシーのぎょうしゅうはんていほう、英: Cauchy condensation test）は標準的な級数の収束判定法の一つである。名称はオーギュスタン＝ルイ・コーシーにちなむ。

各項が非負実数から成る非増加無限数列 ${\displaystyle f(n)}$ に対して、級数 ${\displaystyle \displaystyle \sum \limits _{n=1}^{\infty }f(n)}$ が収束するための必要十分条件は「凝集」した級数 ${\displaystyle \displaystyle \sum \limits _{n=0}^{\infty }2^{n}f(2^{n})}$ が収束することである。さらにこれらの級数が収束するならば、「凝集」した級数の収束値は元の級数の収束値の2倍を上回らない。

級数の評価

コーシーの凝集判定法は、次のより強い評価式から従う。

${\displaystyle \sum _{n=1}^{\infty }f(n)\leq \sum _{n=0}^{\infty }2^{n}f(2^{n})\leq \ 2\sum _{n=1}^{\infty }f(n)}$

（不等式は拡大実数におけるものと考える必要がある。）この証明の中核部分は、ニコル・オレームによる調和級数の発散性の証明に倣っている。

最初の不等式を示すため、元の級数を2の冪乗個ずつの項にくくり直す。くくられたそれぞれの和は、数列の非増加性より、最大値をとる最初の項の値で置き換えた和で上から抑えられる。

${\displaystyle {\begin{array}{rcccccccl}\displaystyle \sum \limits _{n=1}^{\infty }f(n)&=&f(1)&+&f(2)+f(3)&+&f(4)+f(5)+f(6)+f(7)&+&\cdots \\&=&f(1)&+&{\Big (}f(2)+f(3){\Big )}&+&{\Big (}f(4)+f(5)+f(6)+f(7){\Big )}&+&\cdots \\&\leq &f(1)&+&{\Big (}f(2)+f(2){\Big )}&+&{\Big (}f(4)+f(4)+f(4)+f(4){\Big )}&+&\cdots \\&=&f(1)&+&2f(2)&+&4f(4)&+&\cdots \\&=&\sum \limits _{n=0}^{\infty }2^{n}f(2^{n})\end{array}}}$

2番目の不等式を示すため、級数を2の冪乗個ずつの項に再度くくり直す。ただしこのとき以下のように1項ずつくくり方をずらすことで、${\displaystyle \textstyle \sum _{n=0}^{\infty }2^{n}f(2^{n})}$ のそれぞれの括弧内で「最後」に並んでいた ${\displaystyle \textstyle f(2^{n})}$ が、${\displaystyle \textstyle 2\sum _{n=1}^{\infty }f(n)}$ のそれぞれの括弧内では「先頭」に並ぶようにする。

${\displaystyle {\begin{array}{rcl}\sum \limits _{n=0}^{\infty }2^{n}f(2^{n})&=&f(1)+{\Big (}f(2)+f(2){\Big )}+{\Big (}f(4)+f(4)+f(4)+f(4){\Big )}+\cdots \\&=&{\Big (}f(1)+f(2){\Big )}+{\Big (}f(2)+f(4)+f(4)+f(4){\Big )}+\cdots \\&\leq &{\Big (}f(1)+f(1){\Big )}+{\Big (}f(2)+f(2)+f(3)+f(3){\Big )}+\cdots \\&=&2\sum \limits _{n=1}^{\infty }f(n)\end{array}}}$

積分との比較

「凝集」変換 ${\displaystyle \textstyle f(n)\rightarrow 2^{n}f(2^{n})}$ は積分での変数変換 ${\displaystyle \textstyle x\rightarrow e^{x}}$ が ${\displaystyle \textstyle f(x)\,\mathrm {d} x\rightarrow e^{x}f(e^{x})\,\mathrm {d} x}$ を引き起こすことを連想させる。

実際、積分判定法により単調関数 f に対しては級数 ${\displaystyle \sum \limits _{n=1}^{\infty }f(n)}$ の収束と広義積分 ${\displaystyle \displaystyle \int _{1}^{\infty }f(x)\,\mathrm {d} x}$ の収束は同値である。変数変換 ${\displaystyle \textstyle x\rightarrow 2^{x}}$ によって積分は ${\displaystyle \displaystyle \log 2\,\int _{0}^{\infty }\!2^{x}f(2^{x})\,\mathrm {d} x}$ と書き直せるが、この収束は級数 ${\displaystyle \displaystyle \sum \limits _{n=0}^{\infty }2^{n}f(2^{n})}$ の収束と同値になる。

例

この判定法は n が f の分母に現れるような級数に対して役立つことがある。この種の中で最も基本的な例である調和級数 ${\displaystyle \textstyle \sum _{n=1}^{\infty }1/n}$ は級数 ${\displaystyle \textstyle \sum 1}$ へと変換でき、これは明らかに発散する。

より複雑な例として、

${\displaystyle f(n):=n^{-a}(\log n)^{-b}(\log \log n)^{-c}}$

を考える。このとき級数は a > 1 であれば必ず収束し、a < 1 であれば発散する。a = 1 のときは、凝集変換をして整理することで級数

${\displaystyle \sum n^{-b}(\log n)^{-c}}$

が現れる。対数が「左へシフト」していることになる。よってこのときは、b > 1 なら収束、b < 1 なら発散する。b = 1 のときは c の値が議論を左右する。

この結果は容易に一般化できる。凝集判定法を反復して適用することで、${\displaystyle k=1,2,3,\ldots }$ に対する一般化ベルトラン級数（generalized Bertrand series）

${\displaystyle \sum _{n\geq N}{\frac {1}{n\cdot \log n\cdot \log \log n\cdots \log ^{\circ (k-1)}n\cdot (\log ^{\circ k}n)^{\alpha }}}\quad \quad (N=\lfloor \exp ^{\circ k}(0)\rfloor +1)}$

が ${\displaystyle \alpha >1}$ のときは収束し、${\displaystyle 0<\alpha \leq 1}$ のときは発散することを示すことができる^[1]。ここで ${\displaystyle f^{\circ m}}$ は関数 ${\displaystyle f}$ の m 回の反復合成写像

${\displaystyle f^{\circ m}(x):={\begin{cases}f(f^{\circ (m-1)}(x)),&m=1,2,3,\ldots ;\\x,&m=0.\end{cases}}}$

を表す記法である。添字の下限 ${\displaystyle N}$ は、級数の全ての項が正数となるよう選ぶ。注目すべきことに、こうした級数によって任意の遅さで収束または発散する無限和を作ることができる。例えば、${\displaystyle k=2}$ で ${\displaystyle \alpha =1}$ の場合、部分和は ${\displaystyle 10^{10^{100}}}$ 項（1グーゴルプレックス項）足し合わせてようやく 10 を超えるが、それでもなお級数は発散する。

Schlömilchの一般化

u(n) を真に増大する正整数の列で、連続する差分の比が有界である、つまりある正の実数 N があって

${\displaystyle {\Delta u(n) \over \Delta u(n{-}1)}\ =\ {u(n{+}1)-u(n) \over u(n)-u(n{-}1)}\ <\ N\ \ {\text{for all }}n}$

が成り立つものとする。このとき、${\displaystyle f(n)}$ がコーシーの凝集判定法のものと同じ前提条件を満たすなら、級数 ${\displaystyle \textstyle \sum _{n=1}^{\infty }f(n)}$ が収束することと級数

${\displaystyle \sum _{n=0}^{\infty }{\Delta u(n)}\,f(u(n))\ =\ \sum _{n=0}^{\infty }{\Big (}u(n{+}1)-u(n){\Big )}f(u(n))}$

が収束することが同値になる^[2]。

${\displaystyle \textstyle u(n)=2^{n}}$ ととれば ${\displaystyle \textstyle \Delta u(n)=u(n{+}1)-u(n)=2^{n}}$ だから、この命題はコーシーの凝集判定法を特別な場合として含んでいる。

脚注

参考文献

• Bonar, Khoury (2006). Real Infinite Series. Mathematical Association of America. ISBN 0-88385-745-6.

外部リンク

• コーシーの凝集判定法の証明