対数正規分布

対数正規分布

確率密度関数 μ = 0
累積分布関数 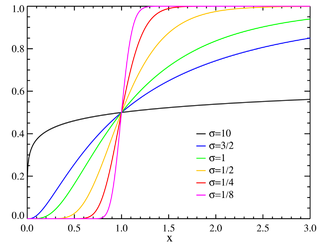μ = 0
母数	${\displaystyle \mu \in \mathbb {R} }$ ${\displaystyle \sigma >0}$
台	${\displaystyle (0,\infty )}$
確率密度関数	${\displaystyle f(x)={\frac {1}{{\sqrt {2\pi }}\sigma x}}\exp \left(-{\frac {(\ln {x}-\mu )^{2}}{2\sigma ^{2}}}\right)}$
累積分布関数	${\displaystyle {\frac {1}{2}}\operatorname {erfc} \!\left[-{\frac {\ln x-\mu }{{\sqrt {2}}\sigma }}\right]}$
期待値	${\displaystyle e^{\mu +\sigma ^{2}/2}}$
中央値	${\displaystyle e^{\mu }}$
最頻値	${\displaystyle e^{\mu -\sigma ^{2}}}$
分散	${\displaystyle e^{2\mu +\sigma ^{2}}(e^{\sigma ^{2}}-1)}$
歪度	${\displaystyle {\sqrt {e^{\sigma ^{2}}-1}}(e^{\sigma ^{2}}+2)}$
尖度	${\displaystyle e^{4\sigma ^{2}}+2e^{3\sigma ^{2}}+3e^{2\sigma ^{2}}-6}$
エントロピー	${\displaystyle {\frac {1}{2}}+{\frac {1}{2}}\ln {(2\pi \sigma ^{2})}+\mu }$
モーメント母関数	-
特性関数	-
テンプレートを表示

確率論および統計学において、対数正規分布（たいすうせいきぶんぷ、英: log-normal distribution）は、連続確率分布の一種である。この分布に従う確率変数の対数をとったとき、対応する分布が正規分布に従うものとして定義される。そのため中心極限定理の乗法的な類似が成り立ち、独立同分布に従う確率変数の積は漸近的に対数正規分布に従う。

定義

平均 μ と標準偏差 σ > 0 に対し、正の実数を値にとる確率変数 X の確率密度関数 f(x) が

${\displaystyle f(x)={\frac {1}{{\sqrt {2\pi \sigma ^{2}}}x}}\exp \left(-{\frac {(\ln x-\mu )^{2}}{2\sigma ^{2}}}\right),\quad 0<x<\infty }$

で与えられるとき、確率変数 X は対数正規分布に従うという。また、上記の確率密度分布に対応する対数正規分布を Λ(μ, σ²) と表記する^[1]。

このとき、対応する分布関数 F(X) は

${\displaystyle {\begin{aligned}F_{X}(x;\mu ,\sigma )&={\frac {1}{2}}\left[1+\operatorname {erf} \!\left({\frac {\ln x-\mu }{\sigma {\sqrt {2}}}}\right)\right]\\&={\frac {1}{2}}\operatorname {erfc} \!\left(-{\frac {\ln x-\mu }{\sigma {\sqrt {2}}}}\right)\\&=\Phi {\bigg (}{\frac {\ln x-\mu }{\sigma }}{\bigg )}\end{aligned}}}$

である。ただし、erfc は相補誤差関数、Φ は標準正規分布の分布関数である。

標準対数正規分布

特に μ = 0, σ² = 1 のとき、この分布は標準対数正規分布と呼ばれる。

つまり標準対数正規分布 Λ(0, 1) は

${\displaystyle f(x)={\frac {1}{{\sqrt {2\pi }}x}}\exp \!\left(-{\frac {(\ln x)^{2}}{2}}\right)}$

なる確率密度関数を持つ確率分布として与えられる。

正規分布との関係

対数正規分布という名は、対数正規分布 Λ(μ, σ²) に従う確率変数 X の対数関数を取ったときに、新たな確率変数 Y = ln X が正規分布 N(μ, σ²) に従うことに由来する。また、正規分布に従う確率変数が負の値を取りうるのに対して、対数正規分布に従う確率変数は正の値のみ取るという性質を有する。

性質

平均・分散

対数正規分布 Λ(μ, σ²) に従う確率変数 X に対し、平均 E(x) および分散 V(x) はそれぞれ以下で与えられる。

${\displaystyle {\begin{aligned}\operatorname {E} (X)&=e^{\mu +\sigma ^{2}/2},\\\operatorname {V} (X)&=e^{2\mu +\sigma ^{2}}(e^{\sigma ^{2}}-1).\end{aligned}}}$

再生性

対数正規分布 Λ(μ₁, σ₁²) に従う確率変数 X と対数正規分布 Λ(μ₂, σ₂²) に従う確率変数 Y が互いに独立であるとき、確率変数の積 XY は対数正規分布 Λ(μ₁ + μ₂, σ₁² + σ₂²) に従う。

この性質は正規分布が再生性を有することから導かれる。

中心極限定理の類似

正の値を取る独立同分布に従う確率変数 X₁, …, X_n が条件

${\displaystyle {\begin{aligned}\mu &=\operatorname {E} (\ln X_{i})<\infty \\\sigma ^{2}&=\operatorname {V} (\ln X_{i})<\infty \end{aligned}}}$

を満たすならば、積 X₁…X_n は漸近的に対数正規分布 Λ(nμ, nσ²) に従う^[2]。

n次対数正規分布

エスペンシェイドらによって提案された次の分布 f_n (x) をn 次対数正規分布 (n-th order log-normal distribution) という^[3]：

${\displaystyle f_{n}(x)=c_{n}x^{n}\exp \left(-{\frac {(\ln x-\ln \mu )^{2}}{2(\ln \sigma )^{2}}}\right)}$

ここで、μ, σ はそれぞれ平均、分散に関する値、c_n は正規化のための定数で

${\displaystyle c_{n}^{-1}={\sqrt {2\pi }}\ln \sigma \mu ^{n+1}\exp \left({\frac {(n+1)^{2}(\ln \sigma )^{2}}{2}}\right)}$

である。通常の対数正規分布は n = −1 次の場合に相当する。

0次対数正規分布

特に0次対数正規分布 (ZOLD)：

${\displaystyle f_{0}(x)={\frac {\exp \left(-{\dfrac {(\ln x-\ln \mu )^{2}}{2(\ln \sigma )^{2}}}\right)}{{\sqrt {2\pi }}\ln \sigma \mu \exp \left({\dfrac {(\ln \sigma )^{2}}{2}}\right)}}}$

は、最頻値が μ に等しく、σ に依存しないことから感覚的な理解が容易で、物理学の分野で用いられることがある。

脚注

参考文献

• 蓑谷千凰彦『統計分布ハンドブック』朝倉書店、2003年。 
• Crow, Edwin L.; Shimizu, Kunio (1988). Lognormal distributions. Statistics: Textbooks and Monographs. 88. Marcel Dekker. ISBN 0-8247-7803-0. MR0939191. Zbl 0644.62014. https://books.google.com/books?id=B8kNa1khS4QC 

関連項目

• 正規分布
• ジブラ法則（英語版）（比例効果の法則）